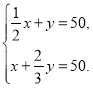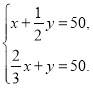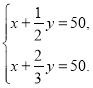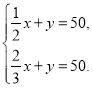题目内容
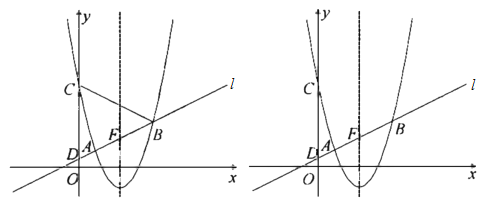
【题目】如图,已知点A(m,m+3),点B(n,n﹣3)是反比例函数y=![]() (k>0)在第一象限的图象上的两点,连接AB.将直线AB向下平移3个单位得到直线l,在直线l上任取一点C,则△ABC的面积为( )
(k>0)在第一象限的图象上的两点,连接AB.将直线AB向下平移3个单位得到直线l,在直线l上任取一点C,则△ABC的面积为( )
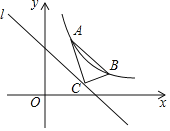
A.![]() B.6C.
B.6C.![]() D.9
D.9
【答案】A
【解析】
由点A(m,m+3),点B(n,n﹣3)在反比例函数y=![]() (k>0)第一象限的图象上,可得到m、n之间的关系,过点A、B分别作x轴、y轴的平行线,构造直角三角形,可求出直角三角形的直角边的长,由平移可得直角三角形的直角顶点在直线l上,进而将问题转化为求△ADB的面积.
(k>0)第一象限的图象上,可得到m、n之间的关系,过点A、B分别作x轴、y轴的平行线,构造直角三角形,可求出直角三角形的直角边的长,由平移可得直角三角形的直角顶点在直线l上,进而将问题转化为求△ADB的面积.
解:∵点A(m,m+3),点B(n,n﹣3)在反比例函数y=![]() (k>0)第一象限的图象上,
(k>0)第一象限的图象上,
∴k=m(m+3)=n(n﹣3),
即:(m+n)(m﹣n+3)=0,
∵m+n>0,
∴m﹣n+3=0,即:m﹣n=﹣3,
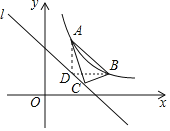
过点A、B分别作x轴、y轴的平行线相交于点D,
∴BD=xB﹣xA=n﹣m=3,AD=yA﹣yB=m+3﹣(n﹣3)=m﹣n+6=3,
又∵直线l是由直线AB向下平移3个单位得到的,
∴平移后点A与点D重合,
因此,点D在直线l上,
∴S△ACB=S△ADB=![]() ADBD=
ADBD=![]() ,
,
故选:A.

练习册系列答案
相关题目