题目内容
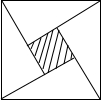
 10、如图,是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形较长的直角边为a,较短的直角边为b,则(a-b)(a2+b2)的值等于
10、如图,是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形较长的直角边为a,较短的直角边为b,则(a-b)(a2+b2)的值等于13
.分析:根据已知可求得四个三角形的面积和,再根据完全平方公式不难求得代数式的值.
解答:解:观察图形,根据勾股定理,知a2+b2即大正方形的面积是13,又根据直角三角形的面积公式,知2ab即其中四个直角三角形的面积和=13-1=12
∵(a-b)2=a2+b2-2ab=13-12=1
∵又a>b
∴a-b=1
∴(a-b)(a2+b2)=13.
∵(a-b)2=a2+b2-2ab=13-12=1
∵又a>b
∴a-b=1
∴(a-b)(a2+b2)=13.
点评:熟悉图形的面积公式,注意各部分与a,b之间的关系.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 如图,是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形的两直角边为a、b,则a+b的值等于
如图,是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形的两直角边为a、b,则a+b的值等于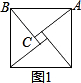

 21、如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为52和4,则直角三角形的两条直角边的长分别为
21、如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为52和4,则直角三角形的两条直角边的长分别为 如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.若图中大小正方形的面积分别为
如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.若图中大小正方形的面积分别为