题目内容
如图,等腰梯形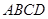 中,AB∥DC,AD=BC=5,DC=7,AB=13,动点P从点A出发,以每秒2个单位的速度沿AD→DC→CB→BA向终点A运动,同时点Q从点B出发,以每秒1个单位的速度沿BA向终点A运动,设运动时间为t秒。(12分)
中,AB∥DC,AD=BC=5,DC=7,AB=13,动点P从点A出发,以每秒2个单位的速度沿AD→DC→CB→BA向终点A运动,同时点Q从点B出发,以每秒1个单位的速度沿BA向终点A运动,设运动时间为t秒。(12分)
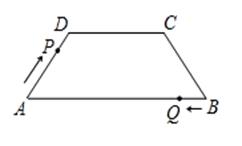
⑴求梯形的高为多少?
⑵分段考虑,当t为何值时,四边形PQBC为平行四边形时?
⑶在整个运动过程中,是否存在某一时刻,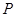 与
与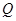 重合?
重合?
【答案】
见解析
【解析】
试题分析: 解:⑴高为4
⑵当点P在AD边上时,PC与BQ不平行,
故此时四边形PQBC不可能为平行四边形;
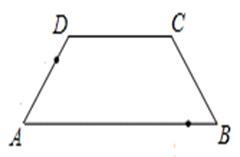
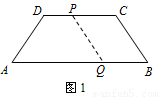
当点P在DC边上时,如图1。
PC=12-2t,BQ=t,
∵四边形PQBC为平行四边形,
∴PC=BQ。
∴12-2t=t,t=4。
∴当t=4时,四边形PQBC为平行四边形。
当点P在BC边上时,PC与BQ不平行,
当点P在AB边上时,PC与BQ不平行。
⑶设时间为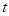 ,
,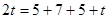
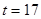
不符合题意。
考点:本题考查了平行四边形的性质定理。
点评:此类试题属于难度较大的试题,主要考查考生对思维变换的把握和平行四边形基本性质的运用。

练习册系列答案
相关题目


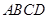 中,
中,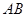 ∥
∥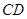 ,
,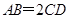 ,
,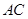 交
交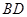 于点
于点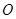 ,点
,点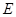 、
、 分别为
分别为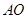 、
、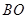 的中点,则下列关于点
的中点,则下列关于点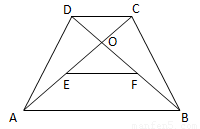
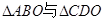 B.
B.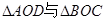
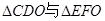 D.
D.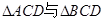
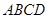 中,
中,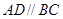 ,
,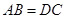 ,
,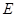 为
为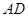 中点,连接
中点,连接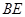 ,
, .
.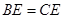 ;
;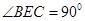 ,过点
,过点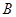 作
作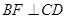 ,垂足为点
,垂足为点 ,交
,交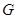 ,连接
,连接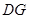 .
.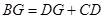 .
.