Question

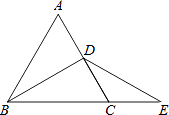
【题目】在△ABC中，∠B=45°，∠C=30°，点D是BC上一点，连接AD，过点A作AG⊥AD，在AG上取点F，连接DF．延长DA至E，使AE=AF，连接EG，DG，且GE=DF．

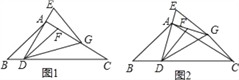
（1）若AB=2，求BC的长；

（2）如图1，当点G在AC上时，求证：BD=CG；

（3）如图2，当点G在AC的垂直平分线上时，直接写出的值．

Answer 1

【答案】（1）BC =2+2;（2）证明见解析;（3）．

【解析】试题分析：（1）如图1中，过点A作AH⊥BC于H，分别在RT△ABH，RT△AHC中求出BH、HC即可．

（2）如图1中，过点A作AP⊥AB交BC于P，连接PG，由△ABD≌△APG推出BD=PG，再利用30度角性质即可解决问题．

（3）如图2中，作AH⊥BC于H，AC的垂直平分线交AC于P，交BC于M．则AP=PC，作DK⊥AB于K，设BK=DK=a，则AK=a，AD=2a，只要证明∠BAD=30°即可解决问题．

试题解析：（1）如图1中，过点A作AH⊥BC于H．

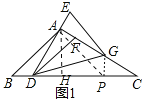
∴∠AHB=∠AHC=90°，

在RT△AHB中，∵AB=2

，∠B=45°，

∴BH=ABcosB=2=2，

AH=ABsinB=2，

在RT△AHC中，∵∠C=30°，

∴AC=2AH=4，CH=ACcosC=2，

∴BC=BH+CH=2+2．

（2）证明：如图1中，过点A作AP⊥AB交BC于P，连接PG，

∵AG⊥AD，∴∠DAF=∠EAC=90°，

在△DAF和△GAE中，

∴△DAF≌△GAE，

∴AD=AG，

∴∠BAP=90°=∠DAG，

∴∠BAD=∠PAG，

∵∠B=∠APB=45°，

∴AB=AP，

在△ABD和△APG中，

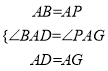
∴△ABD≌△APG，

∴BD=PG，∠B=∠APG=45°，

∴∠GPB=∠GPC=90°，

∵∠C=30°，

∴PG=GC，

∴BD=CG．

（3）如图2中，作AH⊥BC于H，AC的垂直平分线交AC于P，交BC于M．则AP=PC，

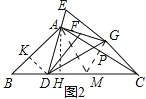
在RT△AHC中，∵∠ACH=30°，

∴AC=2AH，

∴AH=AP，

在RT△AHD和RT△APG中，

∴△AHD≌△APG，

∴∠DAH=∠GAP，

∵GM⊥AC，PA=PC，

∴MA=MC，

∴∠MAC=∠MCA=∠MAH=30°，

∴∠DAM=∠GAM=45°，

∴∠DAH=∠GAP=15°，

∴∠BAD=∠BAH﹣∠DAH=30°，

作DK⊥AB于K，设BK=DK=a，则AK=a，AD=2a，

∴

∵AG=CG=AD，

∴．