题目内容
已知,抛物线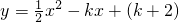 与x轴正半轴交于A、B两点(A点在B点左边),且AB=4.
与x轴正半轴交于A、B两点(A点在B点左边),且AB=4.
(1)求k值;
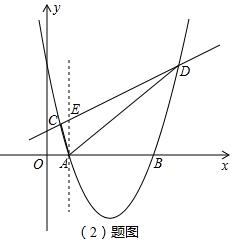
(2)该抛物线与直线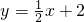 交于C、D两点,求S△ACD;
交于C、D两点,求S△ACD;
(3)该抛物线上是否存在不同于A点的点P,使S△PCD=S△ACD?若存在,求出P点坐标.
(4)若该抛物线上有点P,使S△PCD=tS△ACD,抛物线上满足条件的P点有2个,3个,4个时,分别直接写出t的取值范围.
解:(1)设A(x1,0)、B(x2,0),且x1<x2,x1、x2>0,则:
x1+x2=2k,x1x2=2(k+2)=2k+4
AB=|x1-x2|=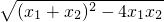 =4,即:k2-2k-8=0
=4,即:k2-2k-8=0
解得:k1=-2,k2=4
∵x1+x2>0,即k>0
 ∴k=4.
∴k=4.
(2)由(1)知,抛物线的解析式:y= x2-4x+6,点A(2,0)、B(6,0);
x2-4x+6,点A(2,0)、B(6,0);
联立直线CD和抛物线的解析式,有:
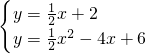 ,
,
解得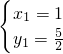 、
、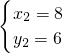
即:C(1, )、D(8,6).
)、D(8,6).
过A作直线AE∥y轴,交直线CD于E,则E(2,3),AE=3;
S△ACD= AE×|yD-yC|=
AE×|yD-yC|= ×3×7=
×3×7= .
.
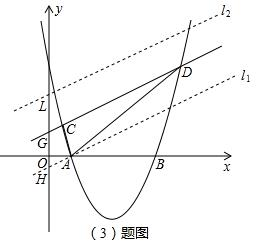 (3)如右图,设直线CD与y轴的交点为G,过点A作l1∥CD交y轴于H,取GH=GL,过L作l2∥CD交y轴于L;
(3)如右图,设直线CD与y轴的交点为G,过点A作l1∥CD交y轴于H,取GH=GL,过L作l2∥CD交y轴于L;
设直线l1:y= x+b1,代入A(2,0),得:
x+b1,代入A(2,0),得:
 ×2+b1=0,b1=-1
×2+b1=0,b1=-1
即,直线l1:y= x-1,H(0,-1),GL=GH=3,L(0,5);
x-1,H(0,-1),GL=GH=3,L(0,5);
同上,可求得,直线l2:y= x+5;
x+5;
联立直线l1与抛物线的解析式,得:
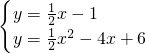 ,
,
解得 、
、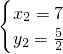
即:P1(7, );
);
联立直线l2与抛物线的解析式,得:
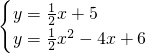 ,
,
解得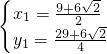 、
、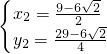
即:P2(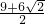 ,
,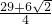 )、P3(
)、P3( ,
,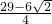 );
);
综上,存在符合条件的P点,且坐标为 P1(7, )、P2(
)、P2(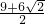 ,
,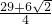 )、P3(
)、P3( ,
,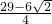 ).
).
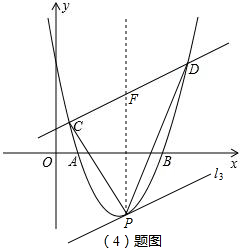 (4)当满足条件的P点有三个时,如右图:
(4)当满足条件的P点有三个时,如右图:
直线l3∥CD,且直线l3与抛物线只有唯一交点P;
设直线l3:y= x+b3,联立抛物线的解析式有:
x+b3,联立抛物线的解析式有:
 x+b3=
x+b3= x2-4x+6,即:x2-9x+12-2b3=0
x2-4x+6,即:x2-9x+12-2b3=0
△=81-4×(12-2b3)=0,解得:b3=-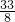
即,直线l3:y= x-
x-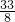 ,P(
,P( ,-
,- );
);
过点P作直线PF∥y轴,交直线CD于F,则F( ,
, )、PF=
)、PF= ;
;
S△PCD= PF×|yD-yC|=
PF×|yD-yC|= ×
× ×7=
×7=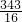 ,t=
,t= =
=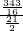 =
=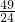 ;
;
综上上面的计算结果和图形来看:
当0<t<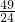 时,P点有四个;
时,P点有四个;
当t=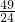 时,P点有三个;
时,P点有三个;
当t>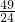 时,P点有两个.
时,P点有两个.
分析:(1)此题要从AB=4入手,若设A、B点的横坐标分别为x1、x2(x1、x2>0),那么显然有等量关系:|x1-x2|=4,即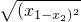 =
=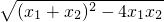 =4,而x1+x2、x1x2可由k表达出来,依据上面的等量关系即可得出k的值.
=4,而x1+x2、x1x2可由k表达出来,依据上面的等量关系即可得出k的值.
(2)首先联立直线CD和抛物线的解析式求出C、D两点的坐标,此时从图上可看出△ACD是一个不规则的三角形,所以可过A作y轴的平行线,交直线CD于E,那么以线段AE为底,C、D横坐标差的绝对值为高即可得出△ACD的面积.
(3)若设直线CD与y轴的交点为G,过点A作直线l1∥CD交y轴于H,然后在y轴上取点L,使得GL=GH,再过L作直线l2∥CD,那么直线l1、l2到直线CD的距离都等于点A到直线CD的距离,所以它们与抛物线的交点都是符合条件的P点.
(4)通过作图可以发现,在直线CD上方肯定有两个P点,所以只考虑直线CD下方的P点个数,这就要抓住P点有三个或直线CD下方有一个P点的情况:P为平行于CD的直线与抛物线的唯一交点;若上述情况(P点有三个)中,t=α,那么:P点有两个时,t>α;P点有三个时,0<t<α.
点评:此题主要考查的是二次函数解析式的确定、二次函数与一元二次方程的联系以及三角形面积的解法;最后一题的难度较大,重点是抓住直线CD下方P点个数的情况,这就要从作图入手来进行分析,由于涉及的情况较多,是容易漏解的地方.
x1+x2=2k,x1x2=2(k+2)=2k+4
AB=|x1-x2|=
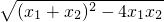 =4,即:k2-2k-8=0
=4,即:k2-2k-8=0解得:k1=-2,k2=4
∵x1+x2>0,即k>0
 ∴k=4.
∴k=4.(2)由(1)知,抛物线的解析式:y=
 x2-4x+6,点A(2,0)、B(6,0);
x2-4x+6,点A(2,0)、B(6,0);联立直线CD和抛物线的解析式,有:
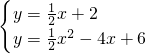 ,
,解得
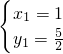 、
、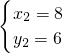
即:C(1,
 )、D(8,6).
)、D(8,6).过A作直线AE∥y轴,交直线CD于E,则E(2,3),AE=3;
S△ACD=
 AE×|yD-yC|=
AE×|yD-yC|= ×3×7=
×3×7= .
. (3)如右图,设直线CD与y轴的交点为G,过点A作l1∥CD交y轴于H,取GH=GL,过L作l2∥CD交y轴于L;
(3)如右图,设直线CD与y轴的交点为G,过点A作l1∥CD交y轴于H,取GH=GL,过L作l2∥CD交y轴于L;设直线l1:y=
 x+b1,代入A(2,0),得:
x+b1,代入A(2,0),得: ×2+b1=0,b1=-1
×2+b1=0,b1=-1即,直线l1:y=
 x-1,H(0,-1),GL=GH=3,L(0,5);
x-1,H(0,-1),GL=GH=3,L(0,5);同上,可求得,直线l2:y=
 x+5;
x+5;联立直线l1与抛物线的解析式,得:
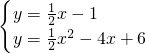 ,
,解得
 、
、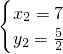
即:P1(7,
 );
);联立直线l2与抛物线的解析式,得:
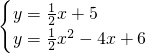 ,
,解得
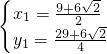 、
、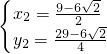
即:P2(
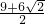 ,
,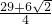 )、P3(
)、P3( ,
,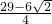 );
);综上,存在符合条件的P点,且坐标为 P1(7,
 )、P2(
)、P2(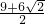 ,
,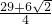 )、P3(
)、P3( ,
,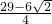 ).
). (4)当满足条件的P点有三个时,如右图:
(4)当满足条件的P点有三个时,如右图:直线l3∥CD,且直线l3与抛物线只有唯一交点P;
设直线l3:y=
 x+b3,联立抛物线的解析式有:
x+b3,联立抛物线的解析式有: x+b3=
x+b3= x2-4x+6,即:x2-9x+12-2b3=0
x2-4x+6,即:x2-9x+12-2b3=0△=81-4×(12-2b3)=0,解得:b3=-
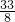
即,直线l3:y=
 x-
x-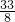 ,P(
,P( ,-
,- );
);过点P作直线PF∥y轴,交直线CD于F,则F(
 ,
, )、PF=
)、PF= ;
;S△PCD=
 PF×|yD-yC|=
PF×|yD-yC|= ×
× ×7=
×7=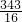 ,t=
,t= =
=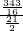 =
=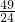 ;
;综上上面的计算结果和图形来看:
当0<t<
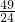 时,P点有四个;
时,P点有四个;当t=
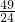 时,P点有三个;
时,P点有三个;当t>
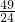 时,P点有两个.
时,P点有两个.分析:(1)此题要从AB=4入手,若设A、B点的横坐标分别为x1、x2(x1、x2>0),那么显然有等量关系:|x1-x2|=4,即
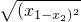 =
=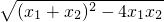 =4,而x1+x2、x1x2可由k表达出来,依据上面的等量关系即可得出k的值.
=4,而x1+x2、x1x2可由k表达出来,依据上面的等量关系即可得出k的值.(2)首先联立直线CD和抛物线的解析式求出C、D两点的坐标,此时从图上可看出△ACD是一个不规则的三角形,所以可过A作y轴的平行线,交直线CD于E,那么以线段AE为底,C、D横坐标差的绝对值为高即可得出△ACD的面积.
(3)若设直线CD与y轴的交点为G,过点A作直线l1∥CD交y轴于H,然后在y轴上取点L,使得GL=GH,再过L作直线l2∥CD,那么直线l1、l2到直线CD的距离都等于点A到直线CD的距离,所以它们与抛物线的交点都是符合条件的P点.
(4)通过作图可以发现,在直线CD上方肯定有两个P点,所以只考虑直线CD下方的P点个数,这就要抓住P点有三个或直线CD下方有一个P点的情况:P为平行于CD的直线与抛物线的唯一交点;若上述情况(P点有三个)中,t=α,那么:P点有两个时,t>α;P点有三个时,0<t<α.
点评:此题主要考查的是二次函数解析式的确定、二次函数与一元二次方程的联系以及三角形面积的解法;最后一题的难度较大,重点是抓住直线CD下方P点个数的情况,这就要从作图入手来进行分析,由于涉及的情况较多,是容易漏解的地方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
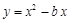 与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
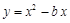 与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.