题目内容
已知:抛物线与x轴交于A(-1,0)、B两点,点B在x轴的正半轴上,与y轴交于点C(0,-3),抛物线顶点为M,连接AC并延长AC交抛物线对称轴于点Q,且点Q到x轴的距离为6.(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,求出点D的坐标.
分析:(1)根据直线A、C的解析式,即可求出直线AC的解析式;已知直线AC上点Q的纵坐标为-6,根据直线AC的解析式即可求出点Q的横坐标即抛物线的对称轴方程;将A、C的坐标代入抛物线的解析式中,联立抛物线的对称轴方程即可求出该抛物线的解析式;
(2)若直线DC与AC垂直,则两条直线的斜率的乘积为-1,由此可确定直线CD的解析式,联立抛物线的解析式即可求出D点的坐标.
(2)若直线DC与AC垂直,则两条直线的斜率的乘积为-1,由此可确定直线CD的解析式,联立抛物线的解析式即可求出D点的坐标.
解答:解:(1)设直线AC的解析式为:y=kx+b(k≠0),则有:
,
解得
;
∴直线AC的解析式为:y=-3x-3;
当y=-6时,-3x-3=-6,x=1;
∴Q(1,-6),即抛物线的对称轴为x=1;
设抛物线的解析式为:y=a(x-1)2+h,依题意,有:
,
解得
∴抛物线的解析式为:y=(x-1)2-4;
(2)由(1)知:直线AC的解析式为:y=-3x-3,若直线CD与AC垂直,
则直线CD的解析式为:y=
x-3,联立抛物线的解析式有:
,
解得
,
;
∴D(
,-
).
|
解得
|
∴直线AC的解析式为:y=-3x-3;
当y=-6时,-3x-3=-6,x=1;
∴Q(1,-6),即抛物线的对称轴为x=1;
设抛物线的解析式为:y=a(x-1)2+h,依题意,有:
|
解得
|
∴抛物线的解析式为:y=(x-1)2-4;
(2)由(1)知:直线AC的解析式为:y=-3x-3,若直线CD与AC垂直,
则直线CD的解析式为:y=
| 1 |
| 3 |
|
解得
|
|
∴D(
| 7 |
| 3 |
| 20 |
| 9 |
点评:此题主要考查了一次函数、二次函数解析式的确定,函数图象交点坐标的求法等知识,需要识记的内容有:如果两条直线互相垂直,那么它们的斜率的乘积为-1.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,
抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C, 与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是
与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是 ,连结AC.
,连结AC.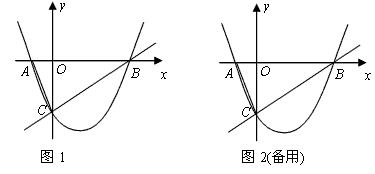
 的顶点坐标是
的顶点坐标是 ]
] 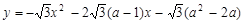 与x轴交于
与x轴交于