题目内容
已知:抛物线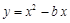 与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
(1)求该抛物线的表达式和点B的坐标;
(2)设C为该抛物线的顶点,⊙C的半径长为2.以该抛物线对称轴上一点P为圆心,线段PO的长为半径作⊙P,如果⊙P与⊙C相切,求点P的坐标.
【答案】
(1)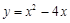 ,(1,-3)或(3,-3)(2)(2,0)、(2,
,(1,-3)或(3,-3)(2)(2,0)、(2, )
)
【解析】解:(1)当y = 0时,得 x1 = 0,x2 = b. ……………………………………(1分)
∴ A(b,0),且b > 0.即得 OA = b.
由 △OAB的面积等于6,B(m,-3),
得  .………………………………………………(1分)
.………………………………………………(1分)
解得 b = 4.
∴ A(4,0),抛物线的表达式为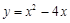 .……………………(2分)
.……………………(2分)
∵ 点B(m,-3)在抛物线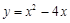 上,
上,
∴ 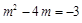 .
.
解得 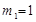 ,
, .
.
∴ 点B的坐标为(1,-3)或(3,-3).…………………………(2分)
(2)∵ 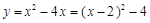 ,
,
∴ 抛物线的顶点为C(2,-4),对称轴为直线x = 2.……………(1分)
设P(2,n).即得  .…………………………………(1分)
.…………………………………(1分)
当⊙P与⊙C相切时,有外切或内切两种情况,并且n > -4.
(ⅰ)如果⊙P与⊙C外切,那么 PC = PO +2.
即得  .
.
解得 n = 0.
∴ P(2,0).…………………………………………………………(2分)
(ⅱ)如果⊙P与⊙C内切,那么 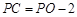 .
.
即得 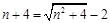 .解得
.解得  .
.
∴ P(2, ).………………………………………………………(2分)
).………………………………………………………(2分)
∴ 所求点P的坐标为(2,0)、(2, ).
).
(1)根据三角形OAB的面积等于6可以求得b = 4的值,从而可知抛物线的解析式;
(2)注意两圆相切有内切和外切两种情况。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
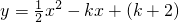 与x轴正半轴交于A、B两点(A点在B点左边),且AB=4.
与x轴正半轴交于A、B两点(A点在B点左边),且AB=4.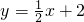 交于C、D两点,求S△ACD;
交于C、D两点,求S△ACD;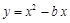 与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.