题目内容
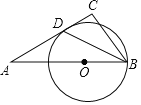
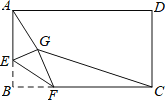
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于点D,交BC于点E,连接ED.
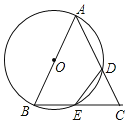
(1)求证:ED=EC;
(2)填空:
①设CD的中点为P,连接EP,则EP与⊙O的位置关系是 ;
②连接OD,当∠B的度数为 时,四边OBED是菱形.
【答案】(1)见解析;(2)①相切;②60°
【解析】
(1)根据等腰三角形的性质和圆内接四边形的性质解答即可;
(2)①如图,连接AE,OE,根据圆周角定理得到AE⊥BC,根据三角形的中位线定理得到OE∥AC,根据平行线的性质得到OE⊥PE,于是得到结论;
②根据已知条件得到△OBE是等边三角形,求得OB=BE,同理OD=DE,根据菱形的判定定理即可得到结论.
解:(1)∵AB=AC,
∴∠B=∠C,
∵∠CDE=∠B,
∴∠CDE=∠C,
∴CE=DE;
(2)①相切;
理由:如图,连接AE,OE,
∵AB是⊙O的直径,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵BO=OA,
∴OE∥AC,
∵DE=CE,PD=CP,
∴PE⊥AC,
∴OE⊥PE,
∴EP与⊙O的位置关系是相切;
②当∠B的度数为60°时,四边OBED是菱形,
∵OB=OE,∠B=60°,
∴△OBE是等边三角形,
∴OB=BE,同理OD=DE,
∴OD=DE=BE=OB,
∴四边OBED是菱形.
故答案为:相切;60°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目