Question

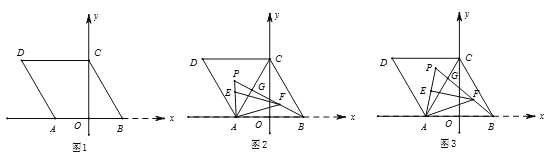
【题目】如图，平面直角坐标系中，直线AB：y=﹣x+b交y轴于点A，交x轴于点B，S△AOB=8．

（1）求点B的坐标和直线AB的函数表达式；

（2）直线a垂直平分OB交AB于点D，交x轴于点E，点P是直线a上一动点，且在点D的上方，设点P的纵坐标为m．

①用含m的代数式表示△ABP的面积；

②当S△ABP=6时，求点P的坐标.

Answer 1

【答案】（1），；（2）①，②

【解析】

（1）可求得直线与两轴相交的两点的坐标为，即，由可求得的值，继而求得点的坐标和直线的解析式；

（2）①由题知直线垂直平分可知，将代入直线的解析式可求得点的坐标，设点的坐标为，然后依据可得到的面积与的函数关系式；②由得到关于的方程可求得的值，从而得到点的坐标；

(1)直线与两轴相交的两点的坐标为，即，

解得

∴点的坐标为

直线的函数表达式：

（2）①∵垂直平分，

∴．

∵将代入得：．

∴点的坐标为．

∵点的坐标为(，

∴．

∵，

∴．

②∵，

∴，解得：．

∴点的坐标为．