题目内容
【题目】已知△ABC中
（1）求作：△ABC的内切圆⊙O（要求尺规作图，保留作图痕迹，不必写作法）
（2）综合应用：在你所作的圆中，若∠AOB=140°，求∠C的度数．
【答案】（1）图形见解析（2）100°
【解析】试题分析：（1）分别作出∠BAC、∠ABC的平分线，两平分线的交点即为△ABC的内切圆的圆心O，过点O向AB作垂线，垂足为H，垂足与O之间的距离即为⊙O的半径，以O为圆心，OH为半径画圆即可；
（2）先根据三角形内角和定理求∠OAB+∠OBA的度数，根据角平分线再求出∠ABC+∠BAC的度数，再由三角形内角和定理即可求解．
试题解析：（1）如图所示，⊙O即为所求；
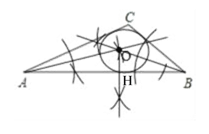
（2）由（1）知，OA、OB分别为∠CAB、∠CBA的平分线，
∴∠CAB=2∠OAB、∠CBA=2∠OBA，
∵∠AOB=140°，
∴∠OAB+∠OBA=40°，
∴∠CAB+∠CBA=2（∠OAB+∠OBA）=80°，
∴∠C=100°．
练习册系列答案
相关题目
