题目内容
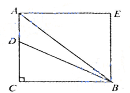
如图,在边长为12的正方形ACBE中,D是边AC上一点,若tan么DBA=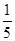 ,则AD的长为( )
,则AD的长为( )
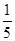 ,则AD的长为( )
,则AD的长为( )
| A.4 | B.2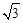 | C.2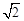 | D.2 |
A
首先由勾股定理得AB=12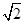 ,
,
在△ABD中,由正弦定理,有: ,
,
由tan∠DBA=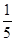 ,得:sin∠DBA=
,得:sin∠DBA= ,cos∠DBA=
,cos∠DBA=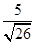 ,
,
而ADB=180°-(45°+∠DBA),由诱导公式得
sin∠ADB=sin(45°+∠DBA)=sin45°×cos∠DBA+cos45°×sin∠DBA=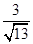 ,
,
所以AD=AB×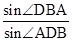 =12
=12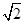 ×
×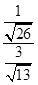 =4,
=4,
故选:A.
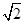 ,
,在△ABD中,由正弦定理,有:
 ,
,由tan∠DBA=
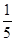 ,得:sin∠DBA=
,得:sin∠DBA= ,cos∠DBA=
,cos∠DBA=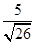 ,
,而ADB=180°-(45°+∠DBA),由诱导公式得
sin∠ADB=sin(45°+∠DBA)=sin45°×cos∠DBA+cos45°×sin∠DBA=
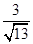 ,
,所以AD=AB×
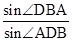 =12
=12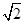 ×
×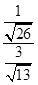 =4,
=4,故选:A.

练习册系列答案
相关题目
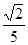 ,则sin∠A=( )。
,则sin∠A=( )。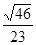

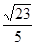
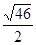
 .
. 中,∠C=90°,sin∠A=
中,∠C=90°,sin∠A=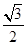 ,则∠A 的度数是 ( )
,则∠A 的度数是 ( ) =
=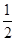 AB·CD,
AB·CD,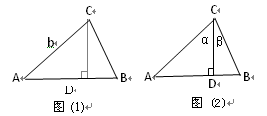
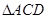 中,
中,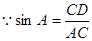 ,
,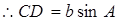
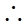
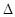 ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.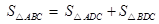 , 由公式①,得
, 由公式①,得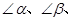
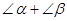 的正弦或余弦函数表示(直接写出结果).
的正弦或余弦函数表示(直接写出结果).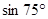 =_________________________
=_________________________ =________
=________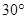 ,此时直升飞机与上海东方明珠底部之间的距离是……………………………………………………( )
,此时直升飞机与上海东方明珠底部之间的距离是……………………………………………………( )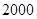 米;
米;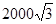 米;
米;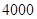 米;
米;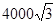 米.
米. 的斜坡向下行驶50米,则它距离地面的垂直高度下降了 米.
的斜坡向下行驶50米,则它距离地面的垂直高度下降了 米.