Question

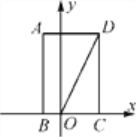
【题目】如图，矩形ABCD的边BC在x轴上，点A在第二象限，点D在第一象限，AB=2，OD=4，将矩形ABCD绕点O旋转，使点D落在x轴上，则点C对应点的坐标是

A. (–，1) B. (–1，) C. (–1，)或(1，–) D. (–，1)或(1，–)

Answer 1

【答案】C

【解析】试题分析：在矩形ABCD中，

∵CD＝AB＝，∠DCO＝90°，OD＝4，

∴OC＝＝2，

①当顺时针旋转至△OD′C′时，如图，OC′＝OC＝2，C′D′＝CD＝，OD′＝OD＝4，

过C′作C′E⊥OD′于E，

OD′·C′E＝OC′·C′D′，

∴C′E＝，

∴OE＝＝＝1，

∴C′（1，－）；

②当逆时针旋转至△OD″C″时，如图，OC″＝OC＝2，C″D″＝CD＝，OD″＝OD＝4，

过C″作C″F⊥OD″于F，

同理可得：C″F＝，OF＝1，

∴C″（－1，）．

综上所述：点C对应点的坐标是（1，－），（－1，），

故选C．