题目内容
4.阅读下列材料,并解决后面的问题.材料:一般地,n个相同的因数a相乘:$\underset{\underbrace{a•a…a}}{n个}$记为an.如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n),如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
问题:(1)计算以下各对数的值:log24=2;log216=4;log264=6.
(2)观察(1)中三数4、16、64之间满足怎样的关系式,然后利用4、16、64之间的数量关系猜想log24、log216、log264之间又满足怎样的关系式?答:log24、log216、log264关系式为log24+log216=log264.
(3)由(2)的结果,请你能归纳出:logaM+logaN=logaM+logaN=logaMN(a>0且a≠1,M>0,N>0).
分析 (1)根据对数的定义求解;
(2)认真观察,不难找到规律:4×16=64,log24+log216=log264;
(3)首先可设logaM=b1,logaN=b2,再根据幂的运算法则:an•am=an+m以及对数的含义,得出结论:logaM+logaN=logaMN.
解答 解:(1)∵22=4,24=16,26=64,
∴log24=2;log216=4;log264=6,
故答案为:2,4,6;
(2)由(1)知,∵2+4=6,
∴log24+log216=log264=log2(4×16),
故答案为:log24+log216=log264;
(3)设logaM=x,logaN=y,
则ax=M,ay=N,
∴MN=ax•ay=ax+y,
∴x+y=logaMN,即logaM+logaN=logaMN
故答案为:logaM+logaN=logaMN.
点评 此题主要考查了数字的变化规律.借考查对数,实际考查学生对指数的理解、掌握的程度;要求学生不但能灵活、准确的应用其运算法则,还要会类比、归纳,推测出对数应有的性质.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
8.关于x的方程kx2-4x+3=0与x轴有交点,则k的范围是( )
| A. | k<$\frac{4}{3}$ | B. | k<$\frac{4}{3}$且k≠0 | C. | k≤$\frac{4}{3}$ | D. | k≤$\frac{4}{3}$且k≠0 |
 如图,一条抛物线经过(-2,5),(0,-3)和(1,-4)三点.
如图,一条抛物线经过(-2,5),(0,-3)和(1,-4)三点.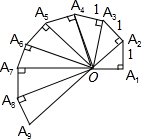 如图是第七届国际数学教育大会的会徽示意图,主题图案是由一连串如图所示的直角三角形演化而成的.其中的第一个三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3…=A8A9=1.
如图是第七届国际数学教育大会的会徽示意图,主题图案是由一连串如图所示的直角三角形演化而成的.其中的第一个三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3…=A8A9=1. +
+ =0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。
=0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。
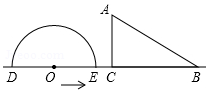 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.