Question

【题目】已知如图，以的边为直径作交斜边于点连接并延长交的延长线于点，点为的中点，连接．

（1）求证：是的切线；

（2）若的半径为，求的长．

Answer 1

【答案】（1）见解析；（2）3．

【解析】

（1）连接FO，由F为BC的中点，AO=CO，得到OF∥AB，由于AC是⊙O的直径，得出CE⊥AE，根据OF∥AB，得出OF⊥CE，于是得到OF所在直线垂直平分CE，推出FC=FE，OE=OC，再由∠ACB=90°，即可得到结论．
（2）证出△AOE是等边三角形，得到∠EOA=60°，再由直角三角形的性质即可得到结果．

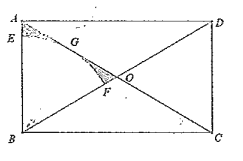
证明：（1）如图1，连接FO，

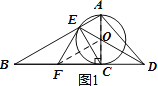
∵F为BC的中点，AO=CO，
∴OF∥AB，
∵AC是⊙O的直径，
∴CE⊥AE，
∵OF∥AB，
∴OF⊥CE，
∴OF所在直线垂直平分CE，
∴FC=FE，OE=OC，
∴∠FEC=∠FCE，∠0EC=∠0CE，
∵∠ACB=90°，
即：∠0CE+∠FCE=90°，
∴∠0EC+∠FEC=90°，
即：∠FEO=90°，
∴FE为⊙O的切线；
（2）如图2，∵⊙O的半径为3，
∴AO=CO=EO=3，
∵∠EAC=60°，OA=OE，
∴∠EOA=60°，

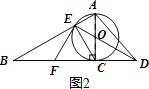
∴∠COD=∠EOA=60°，
∵在Rt△OCD中，∠COD=60°，OC=3，
∴CD=3，
∵在Rt△ACD中，∠ACD=90°，
CD=3，AC=6，
∴AD=3．