��Ŀ����
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=4��BC=3��P������AB�ϵ�һ�����㣬�Ե�PΪԲ�ģ�PAΪ�뾶�ġ�P������AC����һ������ΪD��ֱ��PD��ֱ��BC�ڵ�E��
��1������D��AC���е㣬���P�İ뾶AP�ij���
��2����AP=2����CE�ij���
��3�����߶�BE���е�ΪQ������PQ���P�ཻ�ڵ�I����P���˶��Ĺ����У�����D��C�� I��P����һ��ƽ���ı���ʱ����ֱ��д������AP�ij���
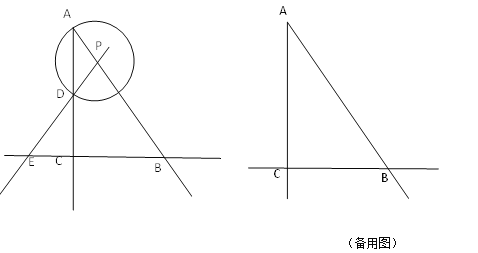
���𰸡���1��AP=![]() ����2��CE=
����2��CE=![]() ����3��AP=
����3��AP=![]() ��AP=
��AP=![]()
�������������������1������P��PF��y���ڵ�F����������Ǻ����Ķ���ó�tan��PAF=![]() =
=![]() =
=![]() ���ٸ��ݴ��������ó�AF�ij������ݹ��ɶ������ɵó����ۣ���2�������������ε��ж������ó���ABC�ס�DEC����Rt��ABC�У����ݹ��ɶ������AB�ij����ٸ���������Ǻ����Ķ��弴�ɵó����ۣ���3�����ݵ�P���߶�AB�ϣ���E���߶�BC�ӳ����ϣ���P���߶�AB�ϣ���E���߶�BC�ϣ���P���߶�AB���ӳ���������������з������ۣ�
���ٸ��ݴ��������ó�AF�ij������ݹ��ɶ������ɵó����ۣ���2�������������ε��ж������ó���ABC�ס�DEC����Rt��ABC�У����ݹ��ɶ������AB�ij����ٸ���������Ǻ����Ķ��弴�ɵó����ۣ���3�����ݵ�P���߶�AB�ϣ���E���߶�BC�ӳ����ϣ���P���߶�AB�ϣ���E���߶�BC�ϣ���P���߶�AB���ӳ���������������з������ۣ�
�����������1������P��PF��y���ڵ�F��

����Rt��ABC��,��ACB=90�㣬AC=4��BC=3��
��tan��PAF=![]() =
=![]() =
=![]() ��
��
�ߵ�D��AC���е㣬
��AD=2��
��AF=1��
��![]() =
=![]() ,���PF=
,���PF=![]() ��
��
��AP=![]() =
=![]() =
=![]() .
.
(2)��AP=DP��
���PAD=��PDA��
�ߡ�PDA=��CDE��
���PAD=��CDE��
�ߡ�ACB=��DCE=90�㣬
���ABC�ס�DEC��
���ABC=��DEC��![]() ��
��
��PB=PE��
Rt��ABC�У���ABC=90�㣬AC=4��BC=3��
��AB=5��
��AP=2��
��PB=PE=3��DE=1
��![]() ��CE=
��CE=![]() ��
��
��3��AP=![]() ��AP=
��AP=![]() ��
��
��AP=x��
�������P���߶�AB�ϣ���E���߶�BC�ӳ�����ʱ����ͼ2����
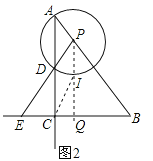
�ɣ�2��֪����ABC�ס�DEC��
��![]()
��![]() ��DC=
��DC=![]() ��5-2x��,
��5-2x��,
��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ���DC=PI�ã�![]() ��5-2x��= x��x=
��5-2x��= x��x=![]() ��
��
�������P���߶�AB�ϣ���E���߶�BC��ʱ����ͼ3����
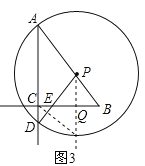
DC=![]() ��2x -5��, ��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ�
��2x -5��, ��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ�
��DC=PI�ã�![]() ��2x -5��= x��x=
��2x -5��= x��x=![]() ��
��
��![]() ��5�����P���߶�AB��ì�ܣ���x=
��5�����P���߶�AB��ì�ܣ���x=![]() ��ȥ��
��ȥ��
�������P���߶�AB���ӳ����ϣ���ͼ4����

��E���߶�BC���ӳ�����ʱ�� DC=![]() ��2x -5��, ��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ���DC=PI�ã�
��2x -5��, ��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ���DC=PI�ã�![]() ��2x -5��= x��x=
��2x -5��= x��x=![]() ��
��