Question

解答下列各题：
（1）已知a=(

1

3

)-1，b=2cos45°+1，c=(2010-π)0，d=|1-

2

|．
①请化简这四个数；
②根据化简结果，列式表示这四个数中“有理数的和”与“无理数的积”的差，然后计算结果．
（2）解方程：

2-x

x-3

+

1

3-x

-1=0
（3）观察右面两个图形，解答下列问题：
①其中是轴对称图形的为

 

，是中心对称图形的为

 

（填序号）；
②用尺规作图的方法画出其中轴对称图形的对称轴（要求：只保留作图痕迹，不写作法）．

Answer 1

分析：（1）①根据负整数指数幂，特殊角的特殊三角函数值，零指数幂以及绝对值即可化简本题，
②根据有理数跟无理数的定义，找出a，c为有理数，b，d为无理数，根据题意计算即可，
（2）观察可得最简公分母是x-3，方程两边乘最简公分母，可以把分式方程转化为整式方程求解，
（3）①根据轴对称图形与中心对称图形的概念分析，②连接关键的对应点，作连线的垂直平分线即可．

解答：解：（1）①a=(

1

3

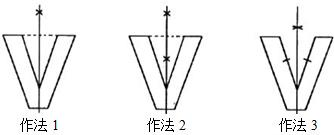
)-1=3，
b=2cos45°+1=2×

2

2

+1=

2

+1，
c=（2010-π）⁰=1，
d=|1-

2

|=

2

-1，
②∵a，c为有理数，b，d为无理数，
∴a+c-bd=3+1-(

2

+1)(

2

-1)
=4-（2-1）=3；

（2）解：方程两边同乘以（x-3），
得2-x-1-（x-3）=0，
解此方程，得x=2，
当x=2时，x-3≠0，
∴x=2是原方程的解，
∴原方程的解是x=2；

（3）解：（1）②，①；
（2）如图：

点评：（1）本题考查了负整数指数幂，特殊角的特殊三角函数值，零指数幂以及绝对值的性质以及有理数跟无理数的定义，
（2）本题考查了分式方程都通过去分母转化成整式方程求解，检验是解分式方程必不可少的一步，
（3）本题考查了轴对称图形和中心对称图形的定义及对称轴的画法，掌握轴对称图形的画法即可．