Question

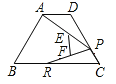
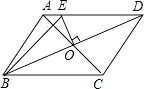
【题目】已知：点P是ABCD的对角线AC的中点，经过点P的直线EF交AB于点E，交DC于点F．求证：AE=CF．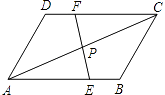

Answer 1

【答案】证明：∵四边形ABCD是平行四边形， ∴AB∥CD，
∴∠PAE=∠PCF，
∵点P是ABCD的对角线AC的中点，
∴PA=PC，
在△PAE和△PCF中，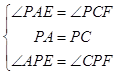
，
∴△PAE≌△PCF（ASA），
∴AE=CF
【解析】由四边形ABCD是平行四边形，易得∠PAE=∠PCF，由点P是ABCD的对角线AC的中点，可得PA=PC，又由对顶角相等，可得∠APE=∠CPF，即可利用ASA证得△PAE≌△PCF，即可证得AE=CF．
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．