题目内容
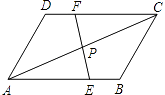
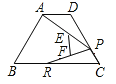
【题目】如图,在梯形ABCD中,AD∥BC,∠ABC=60,AB=DC=2,AD=1,R、P分别是BC、CD边上的动点(点R、B不重合,点P、C不重合),E、F分别是AP、RP的中点,设BR=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是
A. 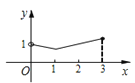 B.
B. 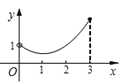 C.
C. 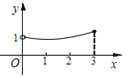 D.
D. 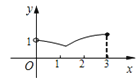
【答案】C
【解析】试题解析:过点A作AG⊥BC,垂足为G,
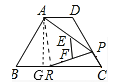
∵∠ABC=60°,AB=2,
∴AG=sin∠ABCAB=![]() ,
,
BG=cos∠ABCAB=![]() ×2=1,
×2=1,
∵BR=x,
∴GR=|x1|,
∴AR2=AG2+GR2=(![]() )2+(1-x)2=4+x2-2x,
)2+(1-x)2=4+x2-2x,
∵E、F分别是AP、RP的中点,
∴EF=![]() AR,
AR,
∴EF2=![]() AR2,
AR2,
∴y2=![]() (4+x2-2x)
(4+x2-2x)
∵y>0,
∴y=![]() ,
,
∵当x=3时,y=![]() ,
,
∴从图象可知A、B、D不符合题意,C符合,
故选C.

练习册系列答案
相关题目