题目内容
如图1,已知:抛物线y=
x2+bx+c与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是y=
x-2,连接AC.
(1)B、C两点坐标分别为B
(2)求证:△AOC∽△COB;
(3)在该抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,请求出来,若不存在,请说明理由.
(4)在该抛物线上是否存在点Q,使得S△ABC=S△ABQ?若存在,请求出来;若不存在,请说明理由.

| 1 |
| 2 |
| 1 |
| 2 |
(1)B、C两点坐标分别为B
(4,0)
(4,0)
、C(0,-2)
(0,-2)
,抛物线的函数关系式为y=
x2-
x-2
| 1 |
| 2 |
| 3 |
| 2 |
y=
x2-
x-2
;| 1 |
| 2 |
| 3 |
| 2 |
(2)求证:△AOC∽△COB;
(3)在该抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,请求出来,若不存在,请说明理由.
(4)在该抛物线上是否存在点Q,使得S△ABC=S△ABQ?若存在,请求出来;若不存在,请说明理由.

分析:(1)在直线的解析式中,令y=0,解得横坐标,即可求得B的坐标,令x=0,解得y的值,则可以求得C的坐标,把B、C的坐标代入解析式,利用待定系数法即可求得二次函数的解析式;
(2)首先求得A的坐标,则OA、OB、OC的长度即可求得,然后根据两组对应边的比相等,且夹角对应相等的三角形相似即可证得;
(3)A关于对称轴的对称点是B,则BC与对称轴的交点就是所求的点;
(4)首先求得△ABC的面积,然后根据三角形的面积公式即可求得Q的纵坐标,然后代入二次函数的解析式即可求得Q的坐标.
(2)首先求得A的坐标,则OA、OB、OC的长度即可求得,然后根据两组对应边的比相等,且夹角对应相等的三角形相似即可证得;
(3)A关于对称轴的对称点是B,则BC与对称轴的交点就是所求的点;
(4)首先求得△ABC的面积,然后根据三角形的面积公式即可求得Q的纵坐标,然后代入二次函数的解析式即可求得Q的坐标.
解答:解:(1)在y=
x-2中,令y=0,则
x-2=0,解得x=4,则B的坐标是(4,0).
令x=0,则y=-2,因而C的坐标是(0,-2).
把B、C的坐标代入二次函数的解析式得:
,解得:
,
则函数的解析式是:y=
x2-
x-2;
(2)在y=
x2-
x-2中,令y=0,则
x2-
x-2=0,解得:x=-1或4,则A的坐标是(-1,0).
因而OA=1,OB=4,OC=2.
则
=
,
又∵∠AOC=∠COB,
∴△AOC∽△COB;
(3)A关于对称轴的对称点是B,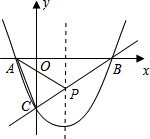
则连接BC,与对称轴的交点就是所求的点P.
抛物线的对称轴是:x=-
=
,
把x=
代入y=
x-2得:y=
-2=-
,
则P的坐标是:(
,-
);
(4)∵S△ABC=
AB•OC=
×5×2=5,
S△ABC=S△ABQ=5,
∴设Q的纵坐标是m,则
AB•|m|=5,即
×5|m|=5,
解得:m=±2,
当m=2时,
x2-
x-2=2,解得:x=
,
当m=-2时,
x2-
x-2=-2,解得:x1=0,x2=3.
则Q的坐标是:(
,2)或(
,2)或(0,-2)或(3,-2).
| 1 |
| 2 |
| 1 |
| 2 |
令x=0,则y=-2,因而C的坐标是(0,-2).
把B、C的坐标代入二次函数的解析式得:
|
|
则函数的解析式是:y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)在y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
因而OA=1,OB=4,OC=2.
则
| OA |
| OC |
| OC |
| OB |
又∵∠AOC=∠COB,
∴△AOC∽△COB;
(3)A关于对称轴的对称点是B,

则连接BC,与对称轴的交点就是所求的点P.
抛物线的对称轴是:x=-
-
| ||
2×
|
| 3 |
| 2 |
把x=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 4 |
则P的坐标是:(
| 3 |
| 2 |
| 5 |
| 4 |
(4)∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
S△ABC=S△ABQ=5,
∴设Q的纵坐标是m,则
| 1 |
| 2 |
| 1 |
| 2 |
解得:m=±2,
当m=2时,
| 1 |
| 2 |
| 3 |
| 2 |
3±
| ||
| 2 |
当m=-2时,
| 1 |
| 2 |
| 3 |
| 2 |
则Q的坐标是:(
3+
| ||
| 2 |
3-
| ||
| 2 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求抛物线解析式和三角形的面积求法.主要考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 如图1,已知:抛物线
如图1,已知:抛物线
 与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是
与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是 ,连结AC.
,连结AC.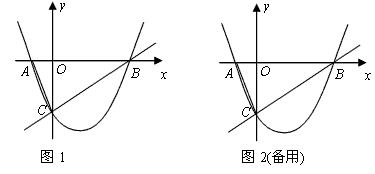
 的顶点坐标是
的顶点坐标是 ]
]