题目内容
阅读下面材料,并解答下列问题:
在形如ab=N的式子中,我们已经研究过两种情况:
①已知a和b,求N,这是乘方运算;
②已知b和N,求a,这是开方运算.
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫作对数运算.
定义:如果ab=N(a>0.a≠1,N>0),则b叫作以a为底的N的对数,记作b=logaN.
例如:因为23=8,所以log28=3;因为2-3=
,所以log2
=-3.
(1)根据定义计算:
①log381=
③log31=
(2)设ax=M,ay=N,则logaN=y(a>0,a≠1,M、N均为正数).用logaM,logaN的代数式分别表示logaMN及loga
,并说明理由.
在形如ab=N的式子中,我们已经研究过两种情况:
①已知a和b,求N,这是乘方运算;
②已知b和N,求a,这是开方运算.
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫作对数运算.
定义:如果ab=N(a>0.a≠1,N>0),则b叫作以a为底的N的对数,记作b=logaN.
例如:因为23=8,所以log28=3;因为2-3=
| 1 |
| 8 |
| 1 |
| 8 |
(1)根据定义计算:
①log381=
4
4
; ②log33=1
1
;③log31=
0
0
; ④如果logx16=4,那么x=±2
±2
.(2)设ax=M,ay=N,则logaN=y(a>0,a≠1,M、N均为正数).用logaM,logaN的代数式分别表示logaMN及loga
| M |
| N |
分析:(1)根据题中给出的对数的运算的定义和法则计算即可;
(2)根据题中给出的对数运算法则总结即可得出下面两个式子的答案.
(2)根据题中给出的对数运算法则总结即可得出下面两个式子的答案.
解答:解:(1)①∵34=81,
∴log381=4;
②∵31=3,
∴log33=1;
③∵30=1,
∴log31=0;
④由题意得:x4=16,
x=±2;
(2)∵ax=M,ay=N,
∴logaM=x,logaN=y,
∵ax•ay=ax+y=MN,
∴logaMN=x+y=logaM+logaN,
∵ax÷ay=ax-y=
,
∴loga
=x-y=logaM-logaN.
∴log381=4;
②∵31=3,
∴log33=1;
③∵30=1,
∴log31=0;
④由题意得:x4=16,
x=±2;
(2)∵ax=M,ay=N,
∴logaM=x,logaN=y,
∵ax•ay=ax+y=MN,
∴logaMN=x+y=logaM+logaN,
∵ax÷ay=ax-y=
| M |
| N |
∴loga
| M |
| N |
点评:此题主要考查了同底数幂的除法,以及对数的计算,关键是同学们要看懂所给例子的计算方法,较好的考查了同学们的观察能力与理解能力.

练习册系列答案
相关题目
 ;
; ;
; .
. 的结果 ;
的结果 ; = ,此时称
= ,此时称 与
与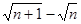 互为有理化因式;
互为有理化因式;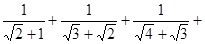 …+
…+  。
。