Question

【题目】（阅读理解）

课外兴趣小组活动时，老师提出了如下问题：

如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：

(1)由已知和作图能得到△ADC≌△EDB的理由是_____.

A.SSS B.SAS C.AAS D.HL

(2)求得AD的取值范围是______.

A.6＜AD＜8 B.6≤AD≤8 C.1＜AD＜7 D.1≤AD≤7

（感悟）

解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.

（问题解决）

(3)如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF.求证：AC＝BF.

Answer 1

【答案】(1)B；(2)C；(3)证明见解析.

【解析】

(1)根据AD＝DE，∠ADC＝∠BDE，BD＝DC推出△ADC和△EDB全等即可；

(2)根据全等得出BE＝AC＝6，AE＝2AD，由三角形三边关系定理得出8﹣6＜2AD＜8+6，求出即可；

(3)延长AD到M，使AD＝DM，连接BM，根据SAS证△ADC≌△MDB，推出BM＝AC，∠CAD＝∠M，根据AE＝EF，推出∠CAD＝∠AFE＝∠BFD，求出∠BFD＝∠M，根据等腰三角形的性质求出即可.

（1）解：在△ADC和△EDB中

，

∴△ADC≌△EDB(SAS)，

故选：B；

（2）解：如图：

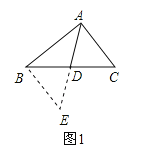
∵由(1)知：△ADC≌△EDB，

∴BE＝AC＝6，AE＝2AD，

∵在△ABE中，AB＝8，由三角形三边关系定理得：8﹣6＜2AD＜8+6，

∴1＜AD＜7，

故选：C.

（3）延长AD到M，使AD＝DM，连接BM，

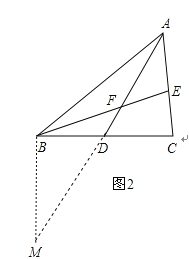
∵AD是△ABC中线，

∴CD＝BD，

∵在△ADC和△MDB中

∴△ADC≌△MDB，

∴BM＝AC，∠CAD＝∠M，

∵AE＝EF，

∴∠CAD＝∠AFE，

∵∠AFE＝∠BFD，

∴∠BFD＝∠CAD＝∠M，

∴BF＝BM＝AC，

即AC＝BF.