题目内容
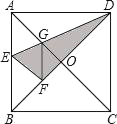
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:
①∠AGD=112.5°;②tan∠AED=![]() +1;③四边形AEFG是菱形;④S△ACD=
+1;③四边形AEFG是菱形;④S△ACD=![]() S△OCD.其中正确结论的序号是__.(把所有正确结论的序号都填在横线上)
S△OCD.其中正确结论的序号是__.(把所有正确结论的序号都填在横线上)
【答案】①②③
【解析】试题分析:∵四边形ABCD是正方形,
∴∠ADB=45°,
由折叠的性质可知,∠ADE=∠BDE=22.5°,
∴∠AGD=180°﹣90°﹣22.5°=112.5°,①正确;
设AE=x,
∵△BEF是等腰直角三角形,
∴BE=![]() EF=
EF=![]() AE=
AE=![]() x,
x,
∴x+![]() x=1,
x=1,
解得,x=![]() ﹣1,
﹣1,
∴tan∠AED=![]() =
=![]() +1,②正确;
+1,②正确;
由同位角相等可知,GF∥AB,EF∥AC,
∴四边形AEFG是平行四边形,
由折叠的性质可知,EA=EF,
∴四边形AEFG是菱形,③正确;
由正方形的性质可知,S△ACD=2S△OCD,④错误,
故答案为:①②③.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目