��Ŀ����
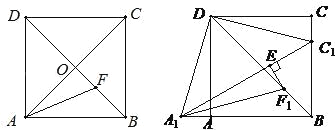
����Ŀ����ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AFƽ�֡�BAC����BD�ڵ�F��
��1����֤��![]() ��
��
��2����A1����C1�ֱ�ͬʱ��A��C�������������ͬ���ٶ��˶���ͬ��ʱ���ͬʱֹͣ����ͼ��A1F1ƽ�֡�BA1C1����BD�ڵ�F1������F1��F1E��A1C1������ΪE�������EF1��AB��![]() ����֮���������ϵ����֤����IJ��룻
����֮���������ϵ����֤����IJ��룻
��3���ڣ�2���������£���A1E��6��C1E��4ʱ����BD�ij�Ϊ������
���𰸡���1���������� ��2��AB��EF1��![]() A1C1 �����ɼ���������3��
A1C1 �����ɼ���������3��![]()
�����������������
��1������ͼ������F��FG��AB�ڵ�G������AFƽ�֡�CAB���ı���ABCD����������֤��AOF�ա�AGF����BGF�ǵ���ֱ�������Σ��ɴ˿ɵ�AO=AG��FG=BG=OF���Ӷ��ɵ�AB=AG+BG=AO+OF=![]() AC+OF�����μ��ɵõ�������
AC+OF�����μ��ɵõ�������
��2������ͼ����F1��F1G1��A1B����F1��F1H1��BC1�ɴ˿ɵ��ı���F1G1BH1�Ǿ��Σ�
����֪������EF1��G1F1��F1H1���Ӷ��ɵ�F1��������A1BC1�����ģ��ɡ�ֱ������������Բ�İ뾶�������߳���Ĺ�ϵ�����CC1=AA1���������EF1��AB��![]() ����֮���������ϵ��
����֮���������ϵ��
��3����ͼ����CC1=AA1=x���ɵ�F1�ǡ�A1BC1�����ģ���E1��G1��H1�����е�ɵ�A1E����A1C1��A1B��BC1����2����A1E��[A1C1����AB��x������AB��x��]��2����10��2x����2��6��
�ɴ˽��x��1��Ȼ����Rt��A1BC1�У���A1B2��BC12��AC12���ɵ�����AB��1��2����AB��1��2��100�����AB�ij�������BD=![]() AB���BD�ij�.
AB���BD�ij�.
���������
��1����F��FG��AB��G��
��AFƽ�֡�CAB��FO��AC��FG��AB��
��OF��FG��
�ߡ�AOF����AGF��90�㣬AF��AF��OF��FG��
���AOF�ա�AGF��
��AO��AG��
ֱ��������BGF�У���DGA��45�㣬
��FG��BG��OF��
��AB��AG��BG��AO��OF��![]() AC��OF��
AC��OF��
��AB��OF��![]() AC��
AC��
��2����F1��F1G1��A1B����F1��F1H1��BC1�����ı���F1G1BH1�Ǿ��Σ�
��BDƽ����ABC��A1F1ƽ�֡�BA1C1��
��F1H1��F1G1=EF1��
����F1��������A1BC1�����ģ�
��EF1����A1B��BC1��A1C1����2����
��A1B��BC1��AB��A1A��BC��CC1����CC1��A1A��
��A1B��BC1��2AB��
��ˢ�ʽ��д�ɣ�EF1����2AB��A1C1����2��
��AB��EF1��![]() A1C1��
A1C1��

��3���ɣ�2���ã�F1��������A1BC1�����ģ���E1��G1��H1�����е㣮
��A1E����A1C1��A1B��BC1����2��
�����CC1��A1A��x��
A1E��[A1C1����AB��x������AB��x��]��2����10��2x����2��6��
��x��1��
��ֱ��������A1BC1�У����ݹ��ɶ�����A1B2��BC12��AC12��
������AB��1��2����AB��1��2��100��
���AB��7��
��BD��7![]() ��
��





