题目内容
如图:(1)在△ABC中,OB、OC分别是∠ABC,∠ACB的平分线,若∠A=x°,求∠BOC的度数;
(2)如图(2),在△ABC中OB,OC分别是△ABC外角∠DBC,∠BCE的角平分线,若∠A=x°,求∠BOC度数;
(3)如图(3),BO,CO分别是△ABC内角∠ABC与外角∠ACD的角平分线,若∠A=x°,求∠BOC的度数.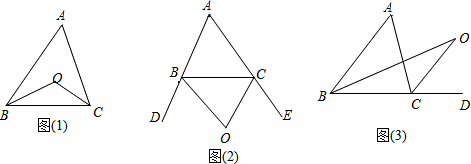
解:(1)∵∠A=x°,
∴∠B+∠C=180°-x°=(180-x)°,
∵OB、OC分别是∠ABC,∠ACB的平分线,
∴∠OBC+∠OCB= (∠B+∠C)=
(∠B+∠C)= (180-x)°
(180-x)°
∴∠BOC=180°-(∠OBC+∠OCB)=180°- (180-x)°=(90+
(180-x)°=(90+ x)°
x)°
(2)∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB
=∠A+∠ACB+∠A+∠ABC
=180°+∠A
=(180+x)°,
∵OB,OC分别是△ABC外角∠DBC,∠BCE的角平分线,
∴∠OBC+∠OCB= (∠DBC+∠ECB)=
(∠DBC+∠ECB)= (180+x)°,
(180+x)°,
∴∠O=180°-(∠OBC+∠OCB)=(90- x)°;
x)°;
(3)∵∠ACD=∠A+∠ACB且BO,CO分别是△ABC内角∠ABC与外角∠ACD的角平分线,
∴∠OCB+∠OBC= ∠ABC+∠ACB+
∠ABC+∠ACB+ ∠ACD=180°-
∠ACD=180°- x°,
x°,
∴∠O=180°-(∠OCB+∠OBC)
=180°-(180°- x°)
x°)
= x°.
x°.
分析:(1)根据∠A的度数,表示出另外两角的和,然后求出它们和的一半,利用三角形内角和定理求得即可;
(2)根据三角形外角的性质和角平分线的性质表示出两个角的和,求出它们的一半,利用三角形内角和定理表示出来即可;
(3)根据三角形外角的性质和角平分线的性质表示出两角和的一半,用180°减去两角和的一半即可.
点评:本题考查了三角形内角和定理及三角形的外角的性质,通过本题目的变式训练能使学生完全掌握此类题目的解法.
∴∠B+∠C=180°-x°=(180-x)°,
∵OB、OC分别是∠ABC,∠ACB的平分线,
∴∠OBC+∠OCB=
 (∠B+∠C)=
(∠B+∠C)= (180-x)°
(180-x)°∴∠BOC=180°-(∠OBC+∠OCB)=180°-
 (180-x)°=(90+
(180-x)°=(90+ x)°
x)°(2)∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB
=∠A+∠ACB+∠A+∠ABC
=180°+∠A
=(180+x)°,
∵OB,OC分别是△ABC外角∠DBC,∠BCE的角平分线,
∴∠OBC+∠OCB=
 (∠DBC+∠ECB)=
(∠DBC+∠ECB)= (180+x)°,
(180+x)°,∴∠O=180°-(∠OBC+∠OCB)=(90-
 x)°;
x)°;(3)∵∠ACD=∠A+∠ACB且BO,CO分别是△ABC内角∠ABC与外角∠ACD的角平分线,
∴∠OCB+∠OBC=
 ∠ABC+∠ACB+
∠ABC+∠ACB+ ∠ACD=180°-
∠ACD=180°- x°,
x°,∴∠O=180°-(∠OCB+∠OBC)
=180°-(180°-
 x°)
x°)
=
 x°.
x°.分析:(1)根据∠A的度数,表示出另外两角的和,然后求出它们和的一半,利用三角形内角和定理求得即可;
(2)根据三角形外角的性质和角平分线的性质表示出两个角的和,求出它们的一半,利用三角形内角和定理表示出来即可;
(3)根据三角形外角的性质和角平分线的性质表示出两角和的一半,用180°减去两角和的一半即可.
点评:本题考查了三角形内角和定理及三角形的外角的性质,通过本题目的变式训练能使学生完全掌握此类题目的解法.

练习册系列答案
相关题目
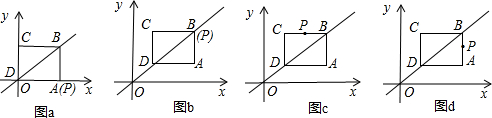
 28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.
28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.