题目内容
计算:① 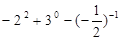 ②a2·a4+(a2)3
②a2·a4+(a2)3
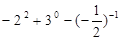 ②a2·a4+(a2)3
②a2·a4+(a2)3(1)-1;(2)2a6.
试题分析:(1)根据平方、零次幂、负整数指数幂的意义进行计算即可求值;
(2)先进行同底数幂的乘法和幂的乘方运算,再进行合并同类项即可求解.
试题解析:(1)原式=-4+1+2=-1;
(2)原式=a6+a6=2a6.
考点: 1.零次幂;2.负整数指数幂;3.同底数幂的乘法;4.幂的乘方.

练习册系列答案
相关题目
题目内容
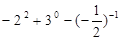 ②a2·a4+(a2)3
②a2·a4+(a2)3