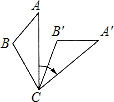
题目内容
已知:用两个边长为3全等的等边三角形△ABC和△ACD拼成菱形ABCD且,把一个含60°的三角尺与这个菱形叠合;如果使三角尺60°的顶点与点A重合,两边分别与AB、AC重合.将三角尺绕A点按逆时针方向旋转(旋转角小于60°).

(1)当三角尺的两边与菱形的两边BC、CD相交于点E、F.
①BE、CF有何数量关系,并证明你的结论.
②接EF,求△CEF面积的最大值.
(2)连接BD,在旋转过程中三角尺的两边分别与BD相交于点M、N,是否存在以BM、MN、ND为边的直角三角形?若存在,求BM的值;若不存在,请说明理由.

(1)当三角尺的两边与菱形的两边BC、CD相交于点E、F.
①BE、CF有何数量关系,并证明你的结论.
②接EF,求△CEF面积的最大值.
(2)连接BD,在旋转过程中三角尺的两边分别与BD相交于点M、N,是否存在以BM、MN、ND为边的直角三角形?若存在,求BM的值;若不存在,请说明理由.
(1)∵△ABC和△ACD为等边三角形,
∴∠B=∠ACD=60°,∠BAC=60°,AB=AC,
又∵∠EAF=60°,且∠BAE=∠BAC-∠AEC=60°-∠AEC,∠CAF=∠EAF-∠AEC=60°-∠AEC,
∴∠BAE=∠CAF,
又∵在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),
∴BE=CF;
(2)∵△ABE≌△ACF,
∴S△ACF=S△ABE,AE=AF,
又∵等边△ABC的边长为3,且S四边形AECF=S△AEC+S△ACF,S△ABC=S△AEC+S△ABE,
∴S四边形AECF=S△ABC=
×3×
=
,
∴S△ECF=S四边形AECF-S△AEF=S△ABC-S△AEF=
-S△AEF,
又∵∠EAF=60°,AE=AF,
∴△AEF为等边三角形,
∴三角尺运动过程中,当AE⊥BC时,S△AEF最小,S△ECF最大,
∴当AE⊥BC时,AE=
,S△AEF=
×
×
=
,
则S△ECF=
-S△AEF═
-
=
;
(3)将△ABM绕点A逆时针旋转120°得到△ADP,其中AM=AP,AB=AD,BM=PD,
∵△ADP≌△ABM,
∴∠PAD=∠BAM,
又∵∠EAF=60°,∠CAD=60°,∠EAC=∠EAF-∠FAC=60°-∠FAC,
∴∠DAF=∠CAD-∠FAC=60°-∠FAC,
∴∠EAC=∠DAF,
∴∠PAN=∠PAD+∠DAF=∠BAM+∠EAC=∠BAC=60°,
又∵在△AMN和△APN中,
,
∴△AMN≌△APN(SAS),
∴MN=PN,
又∵在△PND中,MN=PN,BM=PD,
∴△PND即为以MN,BM,ND为边的三角形,
易知∠PDN=60°,
所以△PND为直角三角形的情况分为两种:
①∠PND=90°,如图4所示,
∵Rt△PND中,∠PDN=60°且BD=3
,
∴ND=
PD,PN=
PD,
则BD=BM+MN+ND=PD+PN+ND,即3
=PD+
PD+
PD,
则BM=PD=3
-3;
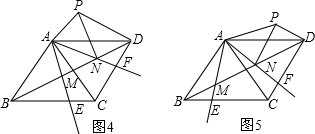
②∠NPD=90°,如图5所示,
∵Rt△PND中,∠PDN=60°且BD=3
,
∴ND=2PD,PN=
PD,
∴BD=BM+MN+ND=PD+PN+ND,即3
=PD+2PD+
PD,
则BM=PD=
.
∴∠B=∠ACD=60°,∠BAC=60°,AB=AC,
又∵∠EAF=60°,且∠BAE=∠BAC-∠AEC=60°-∠AEC,∠CAF=∠EAF-∠AEC=60°-∠AEC,
∴∠BAE=∠CAF,
又∵在△ABE和△ACF中,
|
∴△ABE≌△ACF(ASA),
∴BE=CF;
(2)∵△ABE≌△ACF,
∴S△ACF=S△ABE,AE=AF,
又∵等边△ABC的边长为3,且S四边形AECF=S△AEC+S△ACF,S△ABC=S△AEC+S△ABE,
∴S四边形AECF=S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
9
| ||
| 4 |
∴S△ECF=S四边形AECF-S△AEF=S△ABC-S△AEF=
9
| ||
| 4 |
又∵∠EAF=60°,AE=AF,
∴△AEF为等边三角形,
∴三角尺运动过程中,当AE⊥BC时,S△AEF最小,S△ECF最大,
∴当AE⊥BC时,AE=
3
| ||
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
3
| ||
| 2 |
27
| ||
| 16 |
则S△ECF=
9
| ||
| 4 |
9
| ||
| 4 |
27
| ||
| 16 |
9
| ||
| 16 |
(3)将△ABM绕点A逆时针旋转120°得到△ADP,其中AM=AP,AB=AD,BM=PD,
∵△ADP≌△ABM,
∴∠PAD=∠BAM,
又∵∠EAF=60°,∠CAD=60°,∠EAC=∠EAF-∠FAC=60°-∠FAC,
∴∠DAF=∠CAD-∠FAC=60°-∠FAC,
∴∠EAC=∠DAF,
∴∠PAN=∠PAD+∠DAF=∠BAM+∠EAC=∠BAC=60°,
又∵在△AMN和△APN中,
|
∴△AMN≌△APN(SAS),
∴MN=PN,
又∵在△PND中,MN=PN,BM=PD,
∴△PND即为以MN,BM,ND为边的三角形,
易知∠PDN=60°,
所以△PND为直角三角形的情况分为两种:
①∠PND=90°,如图4所示,
∵Rt△PND中,∠PDN=60°且BD=3
| 3 |
∴ND=
| 1 |
| 2 |
| ||
| 2 |
则BD=BM+MN+ND=PD+PN+ND,即3
| 3 |
| 1 |
| 2 |
| ||
| 2 |
则BM=PD=3
| 3 |

②∠NPD=90°,如图5所示,
∵Rt△PND中,∠PDN=60°且BD=3
| 3 |
∴ND=2PD,PN=
| 3 |
∴BD=BM+MN+ND=PD+PN+ND,即3
| 3 |
| 3 |
则BM=PD=
3
| ||
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目