Question

【题目】正方形A1B1C1O，A2B2C2C1 ， A3B3C3C2 ， …按如图的方式放置．点A1 ， A2 ， A3 ， …和点C1 ， C2 ， C3 ， …分别在直线y=x+1和x轴上，则点B6的坐标是 ．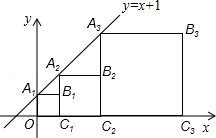

Answer 1

【答案】（63，32）
【解析】方法一：
解：∵直线y=x+1，x=0时，y=1，
∴A1B1=1，点B2的坐标为（3，2），
∴A1的纵坐标是：1=20 ， A1的横坐标是：0=20﹣1，
∴A2的纵坐标是：1+1=21 ， A2的横坐标是：1=21﹣1，
∴A3的纵坐标是：2+2=4=22 ， A3的横坐标是：1+2=3=22﹣1，
∴A4的纵坐标是：4+4=8=23 ， A4的横坐标是：1+2+4=7=23﹣1，
即点A4的坐标为（7，8）．
据此可以得到An的纵坐标是：2n﹣1 ， 横坐标是：2n﹣1﹣1．
即点An的坐标为（2n﹣1﹣1，2n﹣1）．
∴点A6的坐标为（25﹣1，25）．
∴点B6的坐标是：（26﹣1，25）即（63，32）．
所以答案是：（63，32）．
方法二：
∵B1C1=1，B2C2=2，
∴q=2，a1=1，
∴B6C6=25=32，
∴OC1=1=21=1，
OC2=1+2=22﹣1，
OC3=1+2+4=23﹣1…
OC6=26﹣1=63，
∴B6（63，32）．
【考点精析】解答此题的关键在于理解数与式的规律的相关知识，掌握先从图形上寻找规律，然后验证规律，应用规律，即数形结合寻找规律．