题目内容
【题目】已知直线y=﹣2x+4与平面直角坐标系中的x轴、y轴分别交于A、B两点,以AB为边作等腰直角三角形ABC,使得点C与原点O在AB两侧,则点C的坐标为_____.
【答案】(6,2)或(4,6)或(3,3)
【解析】
先根据直线的解析式求出A、B两点的坐标,再根据△ABC是等腰直角三角形,则可分三种情况进行讨论:①A为直角顶点;②B为直角顶点;③C为直角顶点.分别求出点C的坐标即可.
解:∵y=-2x+4,
∴y=0时,-2x+4=0,解得x=2,
x=0时,y=4,
∴A(2,0),B(0,4).
以AB为边作等腰直角三角形ABC,使得点C与原点O在AB两侧,可分三种情况:
①当A为直角顶点时,如图,作CD⊥x轴于点D.
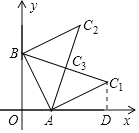
在△ACD和△BAO中,
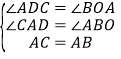 ,
,
∴△ACD≌△BAO(AAS),
∴CD=AO=2,DA=OB=4,
∴OD=OA+AD=2+4=6,
∴C1(6,2);
②当B为直角顶点时,同理可得C2(4,6);
③当C为直角顶点时,显然C3为BC1的中点,则C3(3,3).
综上所述,点C的坐标为(6,2)或(4,6)或(3,3).
故答案为(6,2)或(4,6)或(3,3).

练习册系列答案
相关题目
【题目】我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
指数运算 | 21=2 | 22=4 | 23=8 | … | 31=3 | 32=9 | 33=27 | … |
新运算 | log22=1 | log24=2 | log28=3 | … | log33=1 | log39=2 | log327=3 | … |
根据上表规律,某同学写出了三个式子:①log216=4,②log525=5,③log2 ![]() =﹣1.其中正确的是( )
=﹣1.其中正确的是( )
A.①②
B.①③
C.②③
D.①②③