题目内容
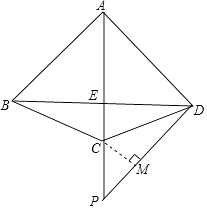
【题目】如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD. 
(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
【答案】
(1)证明:∵AB=AD,AC平分∠BAD,
∴AC⊥BD,
∴∠ACD+∠BDC=90°,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠ADC+∠BDC=90°,
∴∠BDC=∠PDC;
(2)解:过点C作CM⊥PD于点M,
∵∠BDC=∠PDC,
∴CE=CM,
∵∠CMP=∠ADP=90°,∠P=∠P,
∴△CPM∽△APD,
∴ ![]() =
= ![]() ,
,
设CM=CE=x,
∵CE:CP=2:3,
∴PC= ![]() x,
x,
∵AB=AD=AC=1,
∴ ![]() =
= ![]() ,
,
解得:x= ![]() ,
,
故AE=1﹣ ![]() =
= ![]() .
.
【解析】(1)直接利用等腰三角形的性质结合互余的定义得出∠BDC=∠PDC;(2)首先过点C作CM⊥PD于点M,进而得出△CPM∽△APD,求出EC的长即可得出答案.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

 高中必刷题系列答案
高中必刷题系列答案【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= , b=;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为;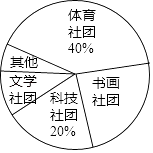
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.






