Question

【题目】如图，△ABC中，BD、CE分别是AC、AB上的中线，BD与CE相交于点O，点M、N分别是OB、OC的中点，连接DE、EM、MN、ND．
（1）求证：四边形DEMN是平行四边形；
（2）若四边形DEMN是菱形，且BC=4cm，AC=6cm，求边AB的长．

Answer 1

【答案】
（1）证明：∵BD、CE分别是AC、AB上的中线，

∴点E为线段AB的中点，点D为线段AC的中点，

∴DE为△ABC的中位线，

∴DE∥BC，且BC=2DE．

∵点M、N分别是OB、OC的中点，

∴MN为△OBC的中位线，

∴MN∥BC，且BC=2MN．

∴DE∥MN，DE=MN，

∴四边形DEMN是平行四边形

（2）作BC边上的中线AF，交BD于M，连接DF，

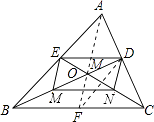
∵BD、AF是边AC、BC上的中线，

∴DF∥BA，DF= BA．

∴△MDF∽△MBA，

∴ = ，

即BD=3DM，

∵四边形DEMN是菱形，且BC=4cm，AC=6cm，

∴EM=DN=MN=2cm，

∴AB=AC=6cm．

【解析】（1）由中位线定理，可得ED∥BC，MN∥BC，且都等于边长BC的一半．分析到此，此题证明即可．（2）根据三角形的中位线定理，得DF∥BA，DF= BA．根据平行得到三角形MDF相似于三角形MBA，再根据相似三角形的对应边的比相等即可求解．
【考点精析】利用三角形中位线定理和平行四边形的判定与性质对题目进行判断即可得到答案，需要熟知连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．