题目内容
【题目】如图,△ABC中,∠ABC=90°.
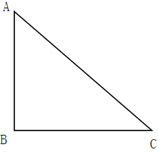
(1)请在BC上找一点P,作⊙P与AC,AB都相切,切点为Q;(尺规作图,保留作图痕迹)
(2)若AB=3,BC=4,求第(1)题中所作圆的半径;
(3)连结BQ,第(2)中的条件均不变,求sin∠CBQ.
【答案】(1)作图见解析;(2)1.5;(3)![]() .
.
【解析】
试题分析:本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了勾股定理、相似三角形的判定与性质和三角函数的定义.(1)作∠BAC的平分线交BC于P点,然后以点P为圆心,PB为半径作圆即可;
(2)连结PQ,如图,先计算出AC=5,设半径为r,BP=PQ=r,PC=4-r,再证明Rt△CPQ∽Rt△CAB,则可利用相似比计算出r即可;
(3)先利用切线长定理得到AB=AQ,加上PB=PQ,则判定AP为BQ的垂直平分线,则利用等角的余角相等得到∠CBQ=∠BAP,然后在Rt△ABP中利用正弦定义求出sin∠BAP,从而可得到sin∠CBQ的值.
试题解析:(1)如图,
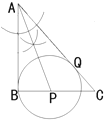 ;
;
(2)连结PQ,设半径为r,BP=PQ=r,PC=4-r,
由∠ABC=90°,AB=3,BC=4,得AC=5,
(易证)△PQC∽△ABC,
![]() =
=![]() ,即
,即![]() =
=![]() ,得r=1.5;
,得r=1.5;
(3)由AB,AQ与⊙P相切,
AB=AQ
BP=PQ
AP为BQ的中垂线
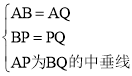 ,
,
易证△BHP∽△ABP,
∠CBQ=∠BAP,
sin∠CBQ=sin∠BAP=![]() .
.


【题目】(10分)校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:
176 118 94 144 102 92 113 105 108 60
115 104 126 158 105 132 114 118 152 104
151 165 102 132 112 114 118 114 168 172
105 118 68 126 128 139 84 136 76 145
134 128 126 110 96 148 146 156 186 182
(1)以20为组距,补充并完成频数分布表;
(2)请补充未完成的频数直方分布图;
(3)若该校七年级有300名学生,请估计60秒能跳绳120次以上的学生有多少人?
次数分组 | 频数 |
60≤ x < 80 | 3 |
80≤ x < 100 | 4 |
100≤ x < 120 | 19 |
140≤ x < 160 | 8 |
180≤ x < 200 | 2 |
合计 | 50 |