题目内容
【题目】如图，已知A（﹣4，﹣1），B（﹣5，﹣4），C（﹣1，﹣3），△ABC经过平移得到的△A′B′C′，△ABC中任意一点P（x1 ， y1）平移后的对应点为P′（x1+6，y1+4）．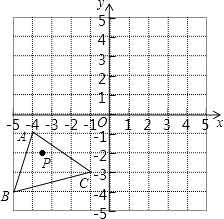
（1）请在图中作出△A′B′C′；
（2）写出点A′、B′、C′的坐标．
（3）求△A′B′C′的面积．
【答案】
（1）解：如图所示；
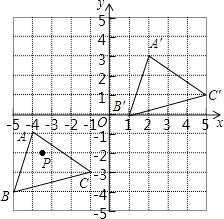
（2）解：由图可知，A′（2，3）、B′（1，0）、C′（5，1）
（3）解：S△A′B′C′=3×4﹣ 
×1×3﹣ ×1×4﹣ ×2×3
=12﹣ 
﹣2﹣3
= 
【解析】①根据△ABC中任意一点平移后的对应点为P'（x1+6，y1+4）可以知道△ABC应向右平移6个单位,向上平移4个单位,由此作出△A'B'C'即可;
②根据各点在坐标系中的位置写出点A'、B'、C'的坐标即可;
③根据△A'B'C'的面积等于长方形的面积减去三个角上三角形的面积即可.
【考点精析】解答此题的关键在于理解坐标与图形变化-平移的相关知识，掌握新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点；连接各组对应点的线段平行且相等．
练习册系列答案
相关题目
