题目内容
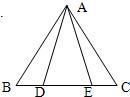22、如图，已知D、E是等腰△ABC底边BC上两点，且BD=CE．求证：∠ADE=∠AED．分析：根据等腰三角形的性质可知AB=AC，∠B=∠C，BD=CE，所以可证△ABD≌△ACE（SAS），所以∠ADB=∠AEC即∠ADE=∠AED．
解答：证明：在等腰△ABC中，
∵AB=AC，
∴∠B=∠C．
又∵BD=CE，
∴△ABD≌△ACE（SAS）．
∴∠ADB=∠AEC．
∴∠ADE=∠AED．
∵AB=AC，
∴∠B=∠C．
又∵BD=CE，
∴△ABD≌△ACE（SAS）．
∴∠ADB=∠AEC．
∴∠ADE=∠AED．
点评：本题主要考查三角形全等的判定方法和等腰三角形的性质．判定两个三角形全等的一般方法有：SSS、SAS、SSA、HL．判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．要掌握利用等腰三角形的性质和全等三角形的性质求线段和角的等量关系的方法．
练习册系列答案
阅读快车系列答案
相关题目
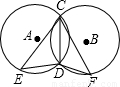
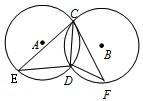7、如图，已知⊙A和⊙B是等圆，CD是它们的公共弦，点E、F分别在⊙A和⊙B上，则∠E和∠F的数量关系是（ ）
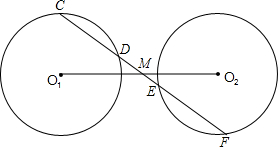助线或另添字母），则M是线段O1O2的中点，并说明理由．（说明理由时可添加辅助线或字母）
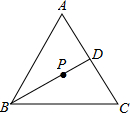（2011•金山区一模）如图，已知：点P是等边△ABC的重心，PD=2，那么AB=
