题目内容
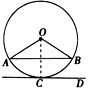
已知如图所示，AB是⊙O的弦，点C在
上。
上。
（1）若∠OAB=34°，求∠AOB的度数；
（2）过C作CD∥AB，若CD是⊙O的切线，求证
（2）过C作CD∥AB，若CD是⊙O的切线，求证
| 解：（1）∵OA=OB， ∴∠OAB=∠OBA 又∵∠OAB=34°， ∴∠AOB=180°-2×34°=112°。 （2）连接OC， ∵CD是⊙O的切线， ∴OC⊥CD 又∵AB∥CD， ∴OC⊥AB ∴  。 |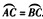
 |
练习册系列答案
相关题目
题目内容
上。
| 解：（1）∵OA=OB， ∴∠OAB=∠OBA 又∵∠OAB=34°， ∴∠AOB=180°-2×34°=112°。 （2）连接OC， ∵CD是⊙O的切线， ∴OC⊥CD 又∵AB∥CD， ∴OC⊥AB ∴ 。 |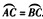
|
26、已知如图所示，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，四边形AEDF是菱形吗？说明理由．
