题目内容
已知关于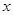 的方程
的方程
(1)求证:无论 取任何实数时,方程恒有实数根;
取任何实数时,方程恒有实数根;
(2)若关于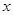 的二次函数
的二次函数 的图象与
的图象与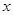 轴两交点间的距离为2时,求抛物线的解析式.
轴两交点间的距离为2时,求抛物线的解析式.
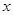 的方程
的方程
(1)求证:无论
 取任何实数时,方程恒有实数根;
取任何实数时,方程恒有实数根;(2)若关于
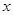 的二次函数
的二次函数 的图象与
的图象与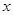 轴两交点间的距离为2时,求抛物线的解析式.
轴两交点间的距离为2时,求抛物线的解析式.(1)分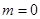 与
与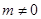 两种情况讨论,再结合一元二次方程的根的判别式即可判断;
两种情况讨论,再结合一元二次方程的根的判别式即可判断;
(2)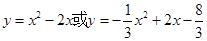
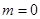 与
与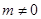 两种情况讨论,再结合一元二次方程的根的判别式即可判断;
两种情况讨论,再结合一元二次方程的根的判别式即可判断;(2)
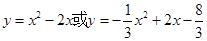
试题分析:(1)分
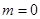 与
与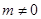 两种情况讨论,再结合一元二次方程的根的判别式即可判断;
两种情况讨论,再结合一元二次方程的根的判别式即可判断;(2)先求出二次函数
 的图象与
的图象与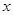 轴的交点坐标,再根据两交点间的距离为2即可求得m的值,从而得到结果.
轴的交点坐标,再根据两交点间的距离为2即可求得m的值,从而得到结果.(1)分两种情况讨论:
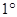 当
当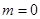 时,方程为
时,方程为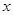
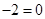 ,
,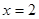 ,方程有实数根
,方程有实数根 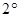 当
当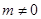 ,则一元二次方程的根的判别式
,则一元二次方程的根的判别式 =
=
不论
 为何实数,
为何实数,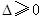 成立,即方程恒有实数根
成立,即方程恒有实数根综合
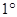 、
、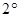 可知
可知 取任何实数,方程
取任何实数,方程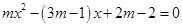 恒有实数根;
恒有实数根;(2)设
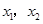 为抛物线
为抛物线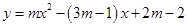 与
与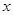 轴交点的横坐标.
轴交点的横坐标.则有
 ,
,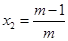
∴抛物线与
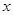 轴交点的坐标为(2 ,0)、(
轴交点的坐标为(2 ,0)、(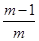 ,0)
,0)∵抛物线与
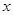 轴两交点间的距离为2
轴两交点间的距离为2∴
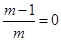 或
或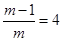
∴
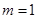 或
或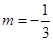
∴所求抛物线的解析式为
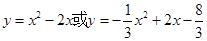 .
.点评:解答本题的关键是熟练掌握一元二次方程
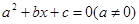 ,当
,当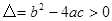 时,方程有两个不相等实数根;当
时,方程有两个不相等实数根;当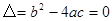 时,方程的两个相等的实数根;当
时,方程的两个相等的实数根;当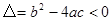 时,方程没有实数根。
时,方程没有实数根。
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

 ?
? 的一个实数根,则该三角形的面积是( )
的一个实数根,则该三角形的面积是( )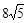
 .
.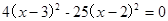
 可以配方成
可以配方成 的形式,那么关于x的方程
的形式,那么关于x的方程 可配方成( )
可配方成( )
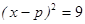

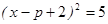
 ;(2)
;(2)
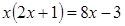 .
.