Question

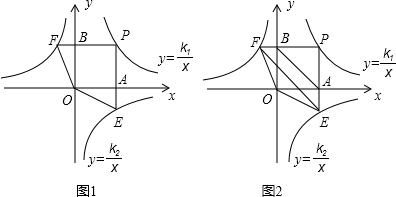
如图，点P是反比例函数y=

k1

x

（k₁＞0，x＞0）图象上一动点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交反比例函数y=

k2

x

（k₂＜0且|k₂|＜k₁）的图象于E、F两点．
（1）图1中，四边形PEOF的面积S₁=

 

（用含k₁、k₂的式子表示）；
（2）图2中，设P点坐标为（2，3）．
①点E的坐标是（

 

，

 

），点F的坐标是（

 

，

 

）（用含k₂的式子表示）；
②若△OEF的面积为

8

3

，求反比例函数y=

k2

x

的解析式．

Answer 1

分析：（1）根据反比例函数中比例系数k的几何意义即可解答；
（2）①根据PE⊥x轴，PF⊥y轴可知，P、E两点的横坐标相同，P、F两点的纵坐标相同，分别把P点的横纵坐标代入反比例函数y=

k2

x

即可求出E、F两点的坐标；
②先根据P点的坐标求出k₁的值，再由E、F两点的坐标用k₂表示出PE、PF的长，再用k₂表示出△PEF的面积，把（1）的结论代入求解即可．

解答：解：（1）∵P是点P是反比例函数y=

k1

x

（k₁＞0，x＞0）图象上一动点，∴S_矩形PBOA=k₁，
∵E、F分别是反比例函数y=

k2

x

（k₂＜0且|k₂|＜k₁）的图象上两点，
∴S_△OBF=S_△AOE=

1

2

|k₂|，
∴四边形PEOF的面积S₁=S_矩形PBOA+S_△OBF+S_△AOE=k₁+|k₂|，
∵k₂＜0，
∴四边形PEOF的面积S₁=S_矩形PBOA+S_△OBF+S_△AOE=k₁+|k₂|=k₁-k₂．

（2）①∵PE⊥x轴，PF⊥y轴可知，P、E两点的横坐标相同，P、F两点的纵坐标相同，
∴E、F两点的坐标分别为E（2，

k2

2

），F（

k2

3

，3）；

②∵P（2，3）在函数y=

k1

x

的图象上，
∴k₁=6，
∵E、F两点的坐标分别为E（2，

k2

2

），F（

k2

3

，3）；
∴PE=3-

k2

2

，PF=2-

k2

3

，
∴S_△PEF=

1

2

（3-

k2

2

）（2-

k2

3

）=

(6-k2)2

12

，
∴S_△OEF=（k₁-k₂）-

(6-k2)2

12

=（6-k₂）-

(6-k2)2

12

=

36-k22

12

=

8

3

，
∵k₂＜0，
∴k₂=-2．
∴反比例函数y=

k2

x

的解析式为y=-

2

x

．

点评：本题难度较大，涉及到反比例函数系数k的几何意义及三角形的面积公式、两点间的距离公式，涉及面较广，难度较大．