题目内容
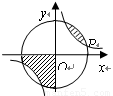
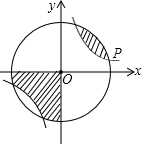 如图,点P(3a,a)是反比例函y=
如图,点P(3a,a)是反比例函y=| k | x |
分析:根据圆的对称性以及反比例函数的对称性可得,阴影部分的面积等于圆的面积的
,即可求得圆的半径,再根据P在反比例函数的图象上,以及在圆上,即可求得k的值.
| 1 |
| 4 |
解答:解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:
πr2=10π
解得:r=2
.
∵点P(3a,a)是反比例函y=
(k>0)与⊙O的一个交点.
∴3a2=k.
=r
∴a2=
×(2
)2=4.
∴k=3×4=12,
则反比例函数的解析式是:y=
.
故答案是:y=
.
| 1 |
| 4 |
解得:r=2
| 10 |
∵点P(3a,a)是反比例函y=
| k |
| x |
∴3a2=k.
| (3a)2+a2 |
∴a2=
| 1 |
| 10 |
| 10 |
∴k=3×4=12,
则反比例函数的解析式是:y=
| 12 |
| x |
故答案是:y=
| 12 |
| x |
点评:本题主要考查了反比例函数图象的对称性,正确根据对称性求得圆的半径是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为 .
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为 .
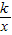 (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为 .
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为 .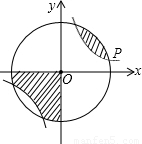
 C.y=
D.y=
C.y=
D.y=