题目内容
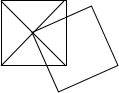 如图所示,边长为a的两个正方形,其中一个正方形的一个顶点恰巧在另一个正方形的中心上,则它们重叠部分(阴影部分)的面积为
如图所示,边长为a的两个正方形,其中一个正方形的一个顶点恰巧在另一个正方形的中心上,则它们重叠部分(阴影部分)的面积为| 1 |
| 4 |
| 1 |
| 4 |
分析:根据正方形性质得出∠ODM=∠OCN=45°,OD=OC,∠DOC=∠NOM=90°,求出∠DOM=∠CON,证△DOM≌△CON(ASA),得出△DOM的面积和△CON的面积相等,推出阴影部分MONC的面积等于△COD的面积,即可求出答案.
解答:解:
∵四边形ABCD和四边形OEFG是正方形,
∴∠ODM=∠OCN=45°,OD=OC,∠DOC=∠NOM=90°,
∴∠DOC-∠MOC=∠NOM-∠MOC,
∴∠DOM=∠CON,
在△DOM和△CON中
,
∴△DOM≌△CON(ASA),
∴△DOM的面积和△CON的面积相等,
即阴影部分MONC的面积等于△COD的面积,
∵△COD的面积是
A2,
∴阴影部分的面积是
a2,
故答案为:
a2.

∵四边形ABCD和四边形OEFG是正方形,
∴∠ODM=∠OCN=45°,OD=OC,∠DOC=∠NOM=90°,
∴∠DOC-∠MOC=∠NOM-∠MOC,
∴∠DOM=∠CON,
在△DOM和△CON中
|
∴△DOM≌△CON(ASA),
∴△DOM的面积和△CON的面积相等,
即阴影部分MONC的面积等于△COD的面积,
∵△COD的面积是
| 1 |
| 4 |
∴阴影部分的面积是
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查了正方形性质,全等三角形的性质和判定的应用,关键是求出△DOM的面积和△CON的面积相等.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则tan∠AED的值等于( )
如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则tan∠AED的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于
如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于 将△OAB绕点O顺时针旋转30°后,得到△OB′A′,点A′恰好落在双曲线y=
将△OAB绕点O顺时针旋转30°后,得到△OB′A′,点A′恰好落在双曲线y= 23、高为50cm,底面周长为50cm的圆柱,在此圆柱的侧面上划分(如图所示)边长为lcm的正方形,用四个边长为lcm的小正方形构成“T”字形,用此图形是否能拼成圆柱侧面?试说明理由.
23、高为50cm,底面周长为50cm的圆柱,在此圆柱的侧面上划分(如图所示)边长为lcm的正方形,用四个边长为lcm的小正方形构成“T”字形,用此图形是否能拼成圆柱侧面?试说明理由. 如图所示,边长为1 的正方形网格中有格点△ABC(顶点是网格线的交点)和格点O,若把△ABC绕点O逆时针旋转90°.
如图所示,边长为1 的正方形网格中有格点△ABC(顶点是网格线的交点)和格点O,若把△ABC绕点O逆时针旋转90°.