题目内容
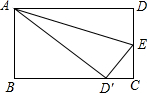
如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.
(1)当x=0时,折痕EF的长为______;当点E与点A重合时,折痕EF的长为______;
(2)试探索使四边形EPFD为菱形时x的取值范围,并求当x=2时,菱形EPFD的边长.提示:用草稿纸折折看,或许对你有所帮助!

(1)当x=0时,折痕EF的长为______;当点E与点A重合时,折痕EF的长为______;
(2)试探索使四边形EPFD为菱形时x的取值范围,并求当x=2时,菱形EPFD的边长.提示:用草稿纸折折看,或许对你有所帮助!

(1)∵纸片折叠,使点D与点P重合,得折痕EF,
当AP=x=0时,点D与点P重合,即为A,D重合,B,C重合,那么EF=AB=CD=3;
当点E与点A重合时,
∵点D与点P重合是已知条件,
∴∠DEF=∠FEP=45°,
∴∠DFE=45°,
即:ED=DF=1,
利用勾股定理得出EF=
∴折痕EF的长为
;
故答案为:3,
;
(2)∵要使四边形EPFD为菱形,
∴DE=EP=FP=DF,
只有点E与点A重合时,EF最长为
,此时x=1,
当EF最短时,即EF=BC,此时x=3,
∴探索出1≤x≤3
当x=2时,如图,连接DE、PF.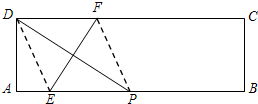
∵EF是折痕,
∴DE=PE,设PE=m,则AE=2-m
∵在△ADE中,∠DAE=90°,
∴AD2+AE2=DE2,即12+(2-m)2=m2
解得m=
,此时菱形EPFD的边长为
.
当AP=x=0时,点D与点P重合,即为A,D重合,B,C重合,那么EF=AB=CD=3;
当点E与点A重合时,
∵点D与点P重合是已知条件,
∴∠DEF=∠FEP=45°,
∴∠DFE=45°,
即:ED=DF=1,
利用勾股定理得出EF=
| 2 |
∴折痕EF的长为
| 2 |
故答案为:3,
| 2 |
(2)∵要使四边形EPFD为菱形,
∴DE=EP=FP=DF,
只有点E与点A重合时,EF最长为
| 2 |
当EF最短时,即EF=BC,此时x=3,
∴探索出1≤x≤3
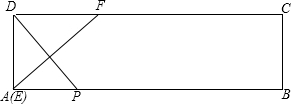
当x=2时,如图,连接DE、PF.

∵EF是折痕,
∴DE=PE,设PE=m,则AE=2-m
∵在△ADE中,∠DAE=90°,
∴AD2+AE2=DE2,即12+(2-m)2=m2
解得m=
| 5 |
| 4 |
| 5 |
| 4 |


练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目