题目内容
如图在直角坐标系中，将矩形OABC沿OB对折，使点A落在点A1处，OB=8，OC=4，则△BDO的面积为______．
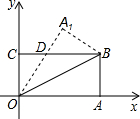
∵BC∥AO，
∴∠BOA=∠OBC，
根据翻折不变性得，∠A1OB=∠BOA，
∴∠OBC=∠A1OB，
∴DO=DB．
设DO=DB=xcm，
则CD=（8-x）cm，
又∵OC=4，
∴（8-x）2+42=x2，
解得x=5．
∴BD=5，
∴S△BDO=
×5×4=10；
故答案为：10．
∴∠BOA=∠OBC，
根据翻折不变性得，∠A1OB=∠BOA，
∴∠OBC=∠A1OB，
∴DO=DB．
设DO=DB=xcm，
则CD=（8-x）cm，
又∵OC=4，
∴（8-x）2+42=x2，
解得x=5．
∴BD=5，
∴S△BDO=
| 1 |
| 2 |
故答案为：10．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
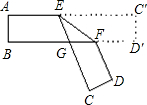
，折叠过程是这样的（阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为26cm，宽为xcm，分别回答下列问题：
