题目内容
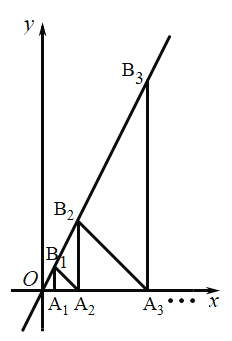
【题目】如图，在坐标轴上取点
，作
轴的垂线与直线
交于点
，作等腰直角三角形
；又过点
作轴的垂线交直线交于点
，作等腰直角三角形
，如此反复作等腰直角三角形，当作到
点时，点的坐标是_____________
【答案】
【解析】
根据点
的坐标和直线解析式即可求出点
的坐标，再根据等腰直角三角形的定义可得
，并求出点
的坐标，同理即可求出点
、
的坐标，找出规律即可归纳出点
的坐标，从而求出结论．
解：过点
作
轴的垂线与直线
交于点，
将x=2代入中，得y=4
∴点的坐标为（2,4）
∴
∵三角形
是等腰直角三角形
∴，点的坐标为（2＋4,0）=（6,0）=（2×31,0）；
同理可得
，点的坐标为（2＋4＋12,0）=（18,0）=（2×32,0）；
，点的坐标为（2＋4＋12＋36,0）=（54,0）=（2×33,0）；
∴点的坐标为（2×3n-1,0）；
∴点
的坐标是
故答案为：．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】如图所示，在OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D，点E在⊙O上，连接CE与⊙O交于点F．
（1）若BC=20，求
的长度；
（2）若EF=AB，求∠OCE的度数．
【题目】为进一步提升教育教学质量，调动学生学习的兴趣，某校在七年级学生中开展了对语文、数学、英语、历史、地理这五门课程的兴趣爱好情况的调查，以便采取必要教学改革，激发学生对各学科的兴趣爱好．随机选取该年级部分学生进行调查，要求每名学生从中选出一门最感兴趣的课程（每名学生只能选一门，不能多选），以下是根据调查结果绘制的不完整统计图表：
课程代号 |
|
|
|
|
|
课程名称 | 语文 | |数学 | 英语 | 历史 | 地理 |
最感兴趣人数 | 12 | 30 |
| 54 | 9 |
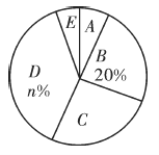
请你根据以上信息，解答下列问题：
（1）被调查学生的总数为______人，
______，
______；
（2）被调查学生中，最喜爱课程的“众数”是______；
（3）若该年级共有800名学生，请估计该年级对语文最感兴趣的学生人数．
