Question

（2012•梁子湖区模拟）已知抛物线y=ax²+bx+3经过A（-3，0），B（-1，0）两点如图1，顶点为M．
（1）a、b的值；
（2）设抛物线与y轴的交点为Q如图1，直线y=-2x+9与直线OM交于点D．现将抛物线平移，保持顶点在直线OD上．当抛物线的顶点平移到D点时，Q点移至N点，求抛物线上的两点M、Q间所夹的曲线

MQ

扫过的区域的面积；
（3）设直线y=-2x+9与y轴交于点C，与直线OM交于点D如图2．现将抛物线平移，保持顶点在直线OD上．若平移的抛物线与射线CD（含端点C）没有公共点时，试探求其顶点的横坐标的取值范围；
（4）如图3，将抛物线平移，当顶点M移至原点时，过点Q（0，3）作不平行于x轴的直线交抛物线于E，F两点．试探究：在y轴的负半轴上是否存在点P，使得∠EPQ=∠QPF？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

分析：（1）将已知的两点的坐标代入二次函数的解析式利用待定系数法求得a、b的值即可；
（2）首先将求得的抛物线的解析式利用配方法求得其顶点坐标，然后求得D点的坐标，3然后利用平移的性质即可求得平行四边形MDNQ的面积；
（3）由（2）知抛物线的顶点M（-2，1），直线OD的解析式为y=

1

2

x，于是设平移的抛物线的顶点坐标为（h，

1

2

h），从而确定平移的抛物线解析式为y=（x-h）²+

1

2

h．然后分当抛物线经过点C和当抛物线与直线CD没有公共点两种情况求得h的值或取值范围即可；
（4）将抛物线平移，当顶点至原点时，其解析式为y=x²，设EF的解析式为y=k x+3（k≠0）．假设存在满足题设条件的点P（0，t）过P作GH∥x轴，分别过E，F作GH的垂线通过证明△GEP∽△HFP得到比例式求得t值即可存在，否则就不存在．

解答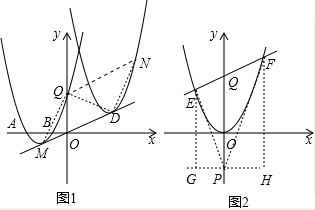：解：（1）抛物线y=ax²+bx+3经过A（-3，0），B（-1，0）两点：
∴

9a-3b+3=0 a-b+3=0

解得：a=1，b=4，
（2）由 （1）求得抛物线的解析式为y=x²+4x+3，
配方得y=（x+2）²-1
∴抛物线的顶点M（-2，-1），
∴直线OD的解析式为y=

1

2

x，
由方程组 

y=-2x+9 y= 1 2 x

，解得：

x= 18 5 y= 9 5

，
∴D（

18

5

，

9

5

）
如图1，由平移的性质知，抛物线上的两点M、Q间所夹的曲线

MQ

扫过的区域的面积即为平行四边形MDNQ的面积，连接QD，
∴S_{平行四边形MDNQ}=2S_△MDQ=2（S_△OQM+S_△OQD）=2×(

1

2

×3×2+

1

2

×3×

18

5

)=

84

5

；
（3）由（2）知抛物线的顶点M（-2，-1），直线OD的解析式为y=

1

2

x，于是设平移的抛物线的顶点坐标为（h，

1

2

h），
∴平移的抛物线解析式为y=（x-h）²+

1

2

h．
①当抛物线经过点C时，
∵C（0，9），
∴h²+

1

2

h=9，解得 h=

-1± 145

4

．
∴当 h＜

-1- 145

4

时，平移的抛物线与射线CD没有公共点．
②当抛物线与直线CD没有公共点时，由方程组

y=(x-h)2+ h 2 y=-2x+9

，
消去y得：x2+(-2h+2)x+h2+

1

2

h-9=0，
∴△=(-2h+2)2-4(h2+

1

2

h-9)＜0，
∴h＞4．
此时抛物线y=（x-4）²+2与直线CD没有公共点．从而与射线CD没有共公点．
综上由①、②可知：平移后的抛物线与射线CD没有公共点时，顶点横坐标的取值范围是：h＜

-1- 145

4

或h＞4
（4）将抛物线平移，当顶点至原点时，其解析式为y=x²，
设EF的解析式为y=k x+3（k≠0）．假设存在满足题设条件的点P（0，t）过P作GH∥x轴，分别过E，F作GH的垂线，
垂足为G，H（如图2）．
∵∠EPQ=∠QPF，
∴∠GEP=∠EPQ=∠QPF=∠HFP，
∴△GEP∽△HFP，
∴

GP

PH

=

GE

HF

，
∴

-xE

xF

=

yE-t

yF-t

=

kxE+3-t

kxF+3-t

∴2k x _E•x _F=（t-3）（x _E+x _F）  
 由

y=x2 y=kx+3

． 得x²-kx-3=0．
∴x_E+x_F=k，x_E•x_F=-3．
∴2k（-3）=（t-3）k
∵k≠0，
∴t=-3．
∴y轴的负半轴上存在点P（0，-3），使∠EPQ=∠QPF．

点评：本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点．主要考查学生数形结合的数学思想方法．