题目内容
【题目】如图,面积为28的平行四边形纸片ABCD中,AB=7,∠BAD=45°,按下列步骤进行裁剪和拼图.

第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
【答案】![]()
【解析】因为△ABE≌△CDF≌△PMQ,∴AE=DF=PM∠EAB=∠FDC=∠MPQ,
∵△ADE≌△BCG≌△PNR,∴AE=BG=PN,∠DAE=∠CBG=∠RPN,
∴PM=PN,∵四边形ABCD是平行四边形,∴∠DAB=∠DCB=45°,
∴∠MPN=90°,∴△MPN是等腰直角三角形,
当PM最小时,对角线MN最小,即AE取最小值,
∴当AE⊥BD时,AE取最小值,
过D作DF⊥AB于F,
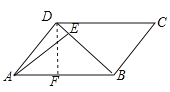
∵平行四边形ABCD的面积为28,AB=7,∴DF=4,
∵∠DAB=45°,∴AF=DF=4,∴BF=3,∴BD=![]() ,
,
∴AE=![]() ,
,
∴MN=![]() .
.

练习册系列答案
相关题目