题目内容
已知二次函数的图象的顶点坐标为(3,-2)且与y轴交于(0,| 5 |
| 2 |
(1)求这个二次函数的解析式,并画于它的图象;
(2)若这抛物线经过点(2,y1),(-1,y2),(
| 7 |
| 2 |
分析:(1)根据题意可设y=a(x-3)2-2,将点(0,
)代入得a=
,求得此物线的解析式;
(2)将x1=2,x2=-1,x3=
代入解析式得y1=-
,y2=6,y3=-
,再比较y1,y2,y3的大小.
| 5 |
| 2 |
| 1 |
| 2 |
(2)将x1=2,x2=-1,x3=
| 7 |
| 2 |
| 3 |
| 2 |
| 15 |
| 8 |
解答: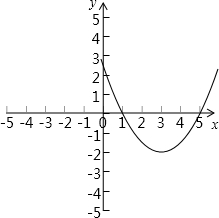 解:(1)可设y=a(x-3)2-2
解:(1)可设y=a(x-3)2-2
将点(0,
)代入得9a-2=
∴a=
∴此抛物线的解析式y=
(x-3)2-2
图象为:
(2)将x1=2,x2=-1,x3=
代入解析式得
y1=-
,y2=6,y3=-
∴y2>y1>y3.
 解:(1)可设y=a(x-3)2-2
解:(1)可设y=a(x-3)2-2将点(0,
| 5 |
| 2 |
| 5 |
| 2 |
∴a=
| 1 |
| 2 |
∴此抛物线的解析式y=
| 1 |
| 2 |
图象为:
(2)将x1=2,x2=-1,x3=
| 7 |
| 2 |
y1=-
| 3 |
| 2 |
| 15 |
| 8 |
∴y2>y1>y3.
点评:本题考查了用待定系数法求函数解析式的方法,当二次函数的顶点坐标已知时,可设顶点式.

练习册系列答案
相关题目



