题目内容
【题目】将连续的奇数1,3,5,7…排列成如下的数表用十字框框出5个数(如图)
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2010吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于355吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.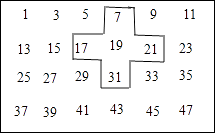
【答案】
(1)解:从表格知道中间的数为a,上面的为a﹣12,下面的为a+12,左面的为a﹣2,右面的为a+2,
a+(a﹣2)+(a+2)+(a﹣12)+(a+12)=5a
(2)解:5a=2010,
a=402,
∵402是偶数,
∴这个是不可以的
(3)解:5a=355,
a=71,
∵71位于一行的最右边,
∴十字框框住的5个数之和不能等于355
【解析】(1)观察中间的数与上下左右四个数字之间的数量关系,再用含a的代数式分别表示出上下左右四个数字。即可求出这5个数之和。
(2)利用(1)得出的结论建立方程求解即可。注意a是中间的数。
(3)利用(1)得出的结论建立方程求解即可。注意a是十字框最中间的数。
【考点精析】掌握数与式的规律是解答本题的根本,需要知道先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律.

练习册系列答案
相关题目