题目内容
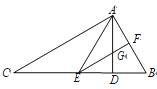
【题目】如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )

A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
【答案】C
【解析】
A选项,∵在△ABC中,点D在BC上,DE∥AC,DF∥AB,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形;即A正确;
B选项,∵四边形AEDF是平行四边形,∠BAC=90°,
∴四边形AEDF是矩形;即B正确;
C选项,因为添加条件“AD平分∠BAC”结合四边形AEDF是平行四边形只能证明四边形AEDF是菱形,而不能证明四边形AEDF是矩形;所以C错误;
D选项,因为由添加的条件“AB=AC,AD⊥BC”可证明AD平分∠BAC,从而可通过证∠EAD=∠CAD=∠EDA证得AE=DE,结合四边形AEDF是平行四边形即可得到四边形AEDF是菱形,所以D正确.
故选C.

练习册系列答案
相关题目