题目内容
【题目】如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是( )
A.10cm
B.30cm
C.60cm
D.50cm
【答案】D
【解析】解:如图,连接OA,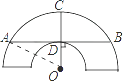
∵CD=10cm,AB=60cm,
∵CD⊥AB,
∴OC⊥AB,
∴AD= ![]() AB=30cm,
AB=30cm,
∴设半径为r,则OD=r﹣10,
根据题意得:r2=(r﹣10)2+302 ,
解得:r=50.
∴这个车轮的外圆半径长为50cm.
故答案为:D.
垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧;根据定理可求得AD= ![]() AB,设半径为r,则OD=r﹣10,用勾股定理可得关于r的方程,解这个方程即可求解。
AB,设半径为r,则OD=r﹣10,用勾股定理可得关于r的方程,解这个方程即可求解。

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目