题目内容
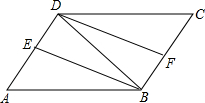 如图,BD是?ABCD的对角线,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DEBF为平行四边形.
如图,BD是?ABCD的对角线,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DEBF为平行四边形.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠CDB=∠ABD,
∵DF平分∠CDB,BE平分∠ABD,
∴∠FDB= ∠CDB,∠EBD=
∠CDB,∠EBD= ∠ABD,
∠ABD,
∴∠FDB=∠EBD,
∴DF∥BE,
∵AD∥BC,即ED∥BF,
∴四边形DEBF是平行四边形.
分析:根据平行四边形性质和角平分线定义求出∠FDB=∠EBD,推出DF∥BE,根据平行四边形的判定判断即可.
点评:本题考查了角平分线定义,平行四边形的性质和判定等的应用,关键是推出DF∥BE,主要检查学生能否运用定理进行推理,题型较好,难度适中.
∴AD∥BC,AB∥CD,
∴∠CDB=∠ABD,
∵DF平分∠CDB,BE平分∠ABD,
∴∠FDB=
 ∠CDB,∠EBD=
∠CDB,∠EBD= ∠ABD,
∠ABD,∴∠FDB=∠EBD,
∴DF∥BE,
∵AD∥BC,即ED∥BF,
∴四边形DEBF是平行四边形.
分析:根据平行四边形性质和角平分线定义求出∠FDB=∠EBD,推出DF∥BE,根据平行四边形的判定判断即可.
点评:本题考查了角平分线定义,平行四边形的性质和判定等的应用,关键是推出DF∥BE,主要检查学生能否运用定理进行推理,题型较好,难度适中.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.
25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数. 如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=
如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=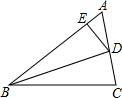 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长. 如图,BD是△ABC的角平分线,且BD=BC=AD.
如图,BD是△ABC的角平分线,且BD=BC=AD. 如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是
如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是