��Ŀ����
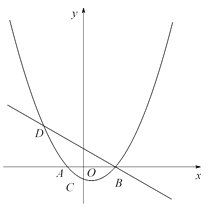
����Ŀ����ͼ����֪������![]() (aΪ��������a��0)��x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��
(aΪ��������a��0)��x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��![]() �������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ��5��
�������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ��5��
��1���������ߵĺ�������ʽ��
��2��PΪֱ��BD�·����������ϵ�һ�㣬����PD��PB, ����PBD��������ֵ��
��3����FΪ�߶�BD��һ��(�����˵�)������AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FD��ÿ��2����λ���ٶ��˶���D��ֹͣ������F�������Ƕ���ʱ����M�������˶���������ʱ���٣�
���𰸡���1��![]() ����2��
����2��![]() ����3����F����Ϊ(��2��
����3����F����Ϊ(��2�� ![]() )ʱ����M�������˶���������ʱ���٣�
)ʱ����M�������˶���������ʱ���٣�
���������������: (1�����������A��B���꣬Ȼ����õ�D���꣬����������y=a��x+2����x-4����aΪ��������a��0������������߽���ʽ��
(2) ��P(m, ![]() ),���������ε������ʽ���ɵý⣻
),���������ε������ʽ���ɵý⣻
��3�������⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+![]() DF���������ߣ���AF+
DF���������ߣ���AF+![]() DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
���������(1)������![]() ��y��0�����x����2��x��4��
��y��0�����x����2��x��4��
��A(��2��0)��B(4��0)��
��ֱ��![]() ������B(4��0)��
������B(4��0)��
��![]() �����
�����![]() ��
��
��ֱ��BD����ʽΪ�� ![]() ��
��
��x����5ʱ��y��3![]() ��
��
��D(��5��3![]() )��
)��
�ߵ�D(��5�� ![]() )��������
)��������![]() �ϣ�
�ϣ�
��![]() ��
��
��![]() ��
��
�������ߵĺ�������ʽΪ�� ![]() ��
��
(2)��P(m, ![]() )
)
��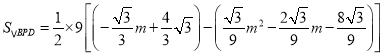
![]() ��
�� ![]()
���BPD��������ֵΪ![]() ����
����
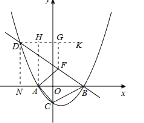
(3)��DK��AB��AH��DK��AH��ֱ��BD�ڵ�F��
����(2)�ã�DN��![]() ,BN��9�����á�DBA��30�������BDH��30����
,BN��9�����á�DBA��30�������BDH��30����
��FG��DF��sin30����![]() ��
��
�൱�ҽ���AH��DKʱ��AF+FH��С��
��M�������˶�����ʱΪ��t��![]() ��
��
��lBD�� ![]() ����Fx��Ax����2��F(��2��
����Fx��Ax����2��F(��2�� ![]() )
)
�൱F����Ϊ(��2�� ![]() )ʱ����ʱ���٣�
)ʱ����ʱ���٣�

 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�