题目内容
如图,已知二次函数![]() 的图像经过点A和点B.
的图像经过点A和点B.
1.求该二次函数的表达式
2.写出该抛物线的对称轴及顶点坐标;
3.点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求P、Q两点的坐标及点Q 到x轴的距离.
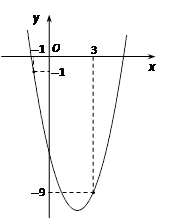
1.将x=-1,y=-1;x=3,y=-9分别代入得
解得
…………………………3分
∴二次函数的表达式为.……………………………4分
2.对称轴为;顶点坐标为(2,-10).………………………………6分
3.将(m,m)代入,得
,
解得.∵m>0,∴
不合题意,舍去.
∴ m=6.………………………………………………………………8分
∴P(6,6);……………………………………………………………9分
∵点P与点Q关于对称轴对称,
∴Q(-2,6)……………………………………………………………11分
∴点Q到x轴的距离为6. ………………………………………………12分
解析:(1)利用待定系数法将A,B两点代入二次函数解析式即可得出a,c的值,得出解析式即可;
(2)利用配方法求出二次函数的顶点坐标和对称轴即可;
(3)利用点P(m,m)在该函数图象上,代入解析式即可求出m的值,进而得出Q到x轴的距离

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C. (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).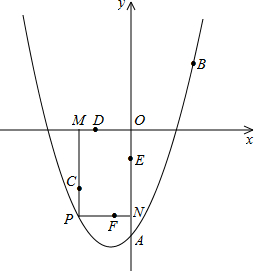 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B( 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4). 如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )
如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )